いきなり本題ですが、本記事では、標準正規分布を一般化したものとしての正規分布、さらに一般化したものとしての多変量正規分布という方向性を持って、標準正規分布を基にした解説を繰り広げていきたいと思います。
当サイトはTwitterやYouTubeでも情報発信しています。ご気軽にフォロー(@AGIRobots)、チャンネル登録お願いします!
標準正規分布
標準正規分布は、正規分布\(N(\mu, \sigma^2)\)において、平均\(\mu=0\)、分散\(\sigma^2=1\)のとしたときの分布で、その確率密度関数は以下のように表されます。
N(x) &=& N(x|\mu=0, \sigma^2=1) \\
&=& \frac{1}{\sqrt{2\pi}}\exp \left (-\frac{x^2}{2}\right )
\end{eqnarray}$$
グラフは図1のようになります。
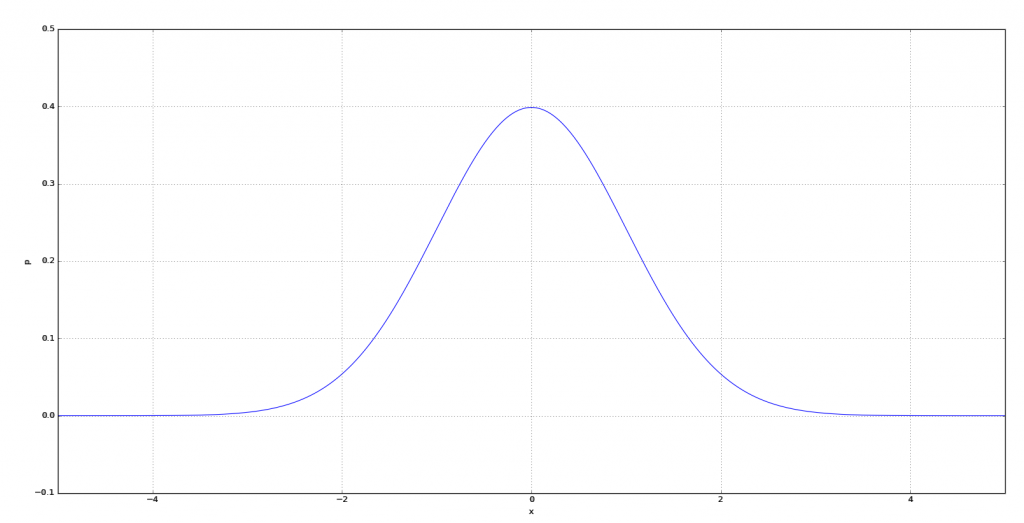
標準正規分布から正規分布へ
正規分布
正規分布は次のような式で表されます。
ここで、平均\(\mu\)と、分散\(\sigma^2\)はパラメータなので、引数として与える必要があります。確率密度関数の例を図2に幾つか示しました。
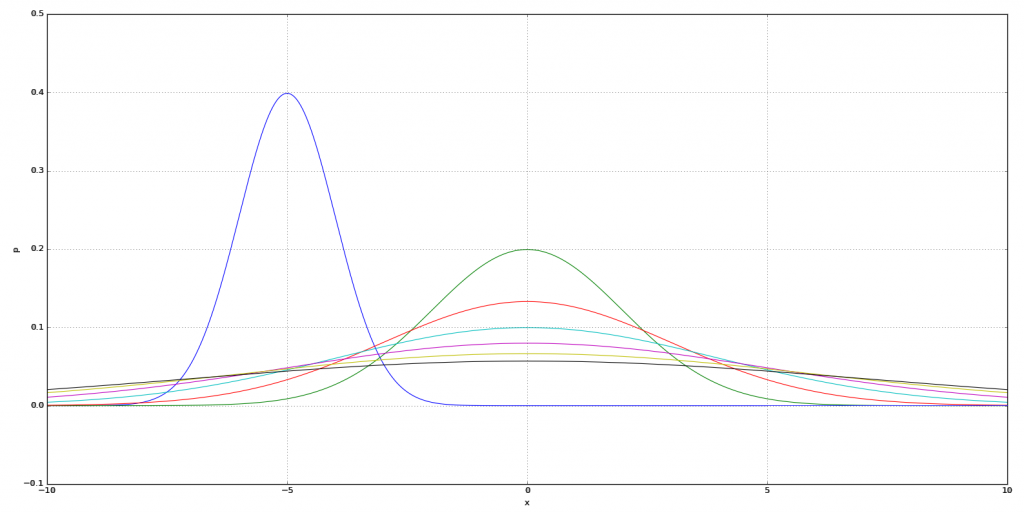
標準正規分布から正規分布を導出
導出では次に示す期待値および分散の3つの性質を使用します。期待値の3つの性質は、
E &=& c \\
E[x + c] &=& E[x] + c \\
E[cx] &=& cE[x]
\end{eqnarray}$$
です。分散の3つの性質は
V &=& 0 \\
V[x + c] &=& V[x] \\
V[cx] &=& c^2V[x]
\end{eqnarray}$$
です。ただし\(c\)は定数とします。
まず、標準正規分布に従う確率変数\(x\)があるとき、
$$E[x] = 0, V[x] = 1$$
が成り立ちます。次に、正規分布\(N(\mu, \sigma^2)\)に従う確率変数を\(x'\)を\(x\)にアフィン変換を施すことで表してみます。すなわち、\(x\)の分布の広がりを\(a\)倍し、\(b\)だけ平行移動したもの、
\(x' = ax + b\)
として表します。このとき、期待値と分散は、先ほどのルールを使って
E[x'] &=& E[ax + b] \\
&=& aE[x] + b \\
&=& b\\
V[x'] &=& V[ax + b] \\
&=& a^2V[x] \\
&=& a^2
\end{eqnarray}$$
と計算できます。正規分布に従う\(x'\)は
\(E[x'] = \mu, V[x'] = \sigma^2\)
を満たすので、\(a = \sigma、b = \mu\)となります。従って、
\(x' = \sigma x + \mu\)
なる変換を施すことで、正規分布が求まることが分かります。上式を\(x\)について解き、標準正規分布の式に代入すると、
$$
\frac{1}{\sqrt{2\pi}}\exp\left\{-\frac{\left (\frac{x' - \mu}{\sigma}\right )^2}{2}\right\}
$$
となります。あとは、積分結果が1になるように、上式を\( (-\infty, \infty)\)で積分した値\(\sigma\)で正規化します。
N(x'|\mu, \sigma^2) = \frac{1}{\sqrt{2\pi}\sigma}\exp \left \{-\frac{(x' - \mu)^2}{2\sigma^2}\right \}
$$
最後に、\(x'\)を\(x\)に置き換えることで、最初に示した正規分布の確率密度関数\(N(x|\mu, \sigma^2)\)
N(x|\mu, \sigma^2) = \frac{1}{\sqrt{2\pi}\sigma}\exp \left \{-\frac{(x - \mu)^2}{2\sigma^2}\right \}
$$
が求まりました。
標準正規分布から多変量正規分布へ
多変量正規分布
多変量正規分布は次の式で表されます。
各成分が確率変数であるベクトル \(\boldsymbol{x} = (x_1, x_2, \cdots, x_d)^T\) の生起確率について示しています。
ここで、\(\boldsymbol{\mu}, \boldsymbol{\Sigma}\)はパラメータです。多変量正規分布の例として2次元正規分布の概形を図3に示します。

標準正規分布から多変量正規分布を導出
それでは、標準正規分布から多変量正規分布を導出していきます。まず、\(\boldsymbol{x} = (x_1, x_2, \cdots, x_d)^T\)の各成分は独立で、それぞれ標準正規分布に従って生起することを仮定します。このとき、\( \boldsymbol{x}\) という状態が生起する確率は、以下の同時確率で表現できます。
Pr(\boldsymbol{x}) &=& \prod_{i=1}^d\frac{1}{\sqrt{2\pi}}\exp\left (-\frac{x_i^2}{2}\right )\\
&=& \frac{1}{(2\pi)^\frac{d}{2}}\exp\left\{-\frac{1}{2}(x_1^2 + x_2^2 + \cdots + x_d^2)\right\}\\
&=& \frac{1}{(2\pi)^\frac{d}{2}}\exp\left (-\frac{1}{2} \boldsymbol{x}^T \boldsymbol{x}\right )
\end{eqnarray} $$
この同時確率の期待値および分散は、
\(E[\boldsymbol{x}] = \boldsymbol{0}, V[\boldsymbol{x}] = \boldsymbol{I}\) ただし\(\boldsymbol{I}\)は単位行列
です。少し説明を加えると、各々の確率変数は標準正規分布に従っているため、
$$
及び、
\(\begin{eqnarray}
V[\boldsymbol{x}] &=& E[(\boldsymbol{x} - E[\boldsymbol{x}]) (\boldsymbol{x} - E[\boldsymbol{x}])^T]\\
&=& E[\boldsymbol{x}\boldsymbol{x}^T]\\
&=& E\left [\begin{pmatrix}
x_1^2 & x_1x_2 & \cdots & x_1x_d\\
x_2x_1 & x_2^2 & \cdots & \vdots\\
\vdots & \vdots & \ddots & \vdots\\
x_dx_1 &\cdots &\cdots & x_d^2
\end{pmatrix}\right ] \\
&=& \boldsymbol{I}
\end{eqnarray}\)
が成り立ちます。後者は任意の\(x_ix_j(i\neq j)\)が独立であること
\(E[x_ix_j] = E[x_i]E[x_j] = 0\)
を使用することで理解することができます。
次に、先ほど標準正規分布から正規分布を導出した時と同様の方針で、多変量正規分布に従う\(\boldsymbol{x'}\)を、\(\boldsymbol{x}\)にアフィン変換を適用した形で考えます。
\(\boldsymbol{x'} = \boldsymbol{Ax} + \boldsymbol{b}\)
このとき、期待値と分散は
\(\begin{eqnarray} E[\boldsymbol{x'}] &=& E[\boldsymbol{Ax} + \boldsymbol{b}] \\ &=& \boldsymbol{A}E[\boldsymbol{x}] + \boldsymbol{b}\\ &=& \boldsymbol{b}\end{eqnarray}\)
\(\begin{eqnarray}
V[\boldsymbol{x'}] &=& V[\boldsymbol{Ax} + \boldsymbol{b}]\\
&=& V[\boldsymbol{Ax}]\\
&=& E[\boldsymbol{Ax}(\boldsymbol{Ax})^T]\\
&=& E[\boldsymbol{Axx}^T\boldsymbol{A}^T]\\
&=& \boldsymbol{A}E[\boldsymbol{xx}^T]\boldsymbol{A}^T\\
&=& \boldsymbol{AA}^T
\end{eqnarray}\)
です。ここで、以下の条件
\(E[\boldsymbol{x'}] = \boldsymbol{\mu}, V[\boldsymbol{x'}] = \boldsymbol{\Sigma}\)
を満たすことから、\(\boldsymbol{b} = \boldsymbol{\mu}, \boldsymbol{AA}^T = \boldsymbol{\Sigma}\)となることが分かります。これを念頭に、\( \boldsymbol{x'} = \boldsymbol{Ax} + \boldsymbol{b}\)を\( \boldsymbol{x}\)について解くと、
\( \boldsymbol{x} = \boldsymbol{A}^{-1}( \boldsymbol{x'} - \boldsymbol{b} ) \)
です。これを、元の式の\(\boldsymbol{x}\)に代入します。
f &\equiv& \frac{1}{(2\pi)^\frac{d}{2}}\exp\left (-\frac{1}{2} \boldsymbol{x}^T \boldsymbol{x}\right )\\
&=& \frac{1}{(2\pi)^\frac{d}{2}}\exp\left (-\frac{1}{2} \boldsymbol{(x' - b)^T(A^{-1})^T} \boldsymbol{A^{-1}(x' - b)}\right ) \\
&=& \frac{1}{(2\pi)^\frac{d}{2}}\exp\left (-\frac{1}{2} \boldsymbol{(x' - b)}^T \boldsymbol{(AA^T)^{-1}} \boldsymbol{(x' - b)}\right ) \\
&=& \frac{1}{(2\pi)^\frac{d}{2}}\exp\left (-\frac{1}{2} \boldsymbol{(x' - b)}^T \boldsymbol{\Sigma^{-1}} \boldsymbol{(x' - b)}\right )
\end{eqnarray} $$
最後に、確率密度関数の性質である積分結果が1を満たすように正規化係数を導出し分母に追加します。上式を\(\int f(x)dx\)で積分すると値は\(\sqrt{\det (\Sigma)}\)になるので、正規化係数は\(\sqrt{\det (\Sigma)}\) です。分母にかけると、以下のような式になります。
Pr(\boldsymbol{x'}) &=& \frac{1}{\int f(x)dx}f(x)\\
&=& \frac{1}{(2\pi)^\frac{d}{2} \sqrt{\det (\Sigma)} }\exp\left (-\frac{1}{2} \boldsymbol{(x' - \mu)}^T \boldsymbol{\Sigma^{-1}} \boldsymbol{(x' - \mu)}\right )
\end{eqnarray} $$
ここで、\(\boldsymbol{x'}\)から、 \(\boldsymbol{x}\) に置き換えれば、多変量正規分布の確率密度関数
が求まります。
まとめ
本記事では、標準正規分布から、正規分布や多変量正規分布を求める形で解説を進めてきました。これら3つは重要な式なので再掲します。
標準正規分布
N(x) &=& N(x|\mu=0, \sigma^2=1) \\
&=& \frac{1}{\sqrt{2\pi}}\exp \left (-\frac{x^2}{2}\right )
\end{eqnarray}$$
正規分布
多変量正規分布
本記事の内容は以上になります。
最後までお読みいただきありがとうございました。
