本記事では、ニューラルネットワークの中間層で線形関数を使用するとネットワークの表現能力が低下する理由について解説していきたいと思います。
2層NNと3層NNの等価条件
ここでは、以下の図のような2層NNと3層NNの等価条件について数式を使用して示していきます。
※ニューラルネットワークの総数に入力層を含むかどうかは議論がありますが、本記事では含めて考えてみました。

では、上記2つのニューラルネットの出力式を定式化していきます。その際に、中間層の活性化関数を\(\phi(・)\)、出力層の活性化関数を\(\psi(・)\)、 中間層ノードの閾値を\(b\)、出力層ノードの閾値を\(c\)とします。
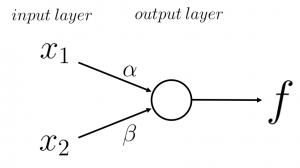
図1に示した2層NNの出力式
図1に示す2層NNは、入力として\(x_1\)と\(x_2\)を受け取り、出力層の出力値\(f\)を求めています。
これは、
$$
f_2 = \psi(\alpha x_1 + \beta x_2 + c)
$$
で表されます。
図2に示した3層NNの出力式
図2に示す3層NNは、入力として\(x_1\)と\(x_2\)を受け取り、中間層の各ノードの出力値\(h_1\)と\(h_2\)を求め、出力層の出力値\(f\)を求めています。
中間層にある2つのニューロンの出力値は
$$\begin{eqnarray}
h_1 &=& \phi(v_{11}x_1 + v_{21}x_2 + b_1)\\
h_2 &=& \phi(v_{12}x_1 + v_{22}x_2 + b_2)
\end{eqnarray}$$
で表すことができます。出力層の出力値\(f\)は\(h_1\)と\(h_2\)を使って、
$$
f_3 = \psi(w_1h_1 + w_2h_2 + c)
$$
と表すことができます。
2つのNNが等価になる条件
上で示した2層NNと3層NNの出力式
$$\begin{eqnarray}
f_2 &=& \psi(\alpha x_1 + \beta x_2 + c)\\
f_3 &=& \psi(w_1h_1 + w_2h_2 + c)
\end{eqnarray}$$
が等しいと仮定して、等価条件を求めていきます。等価であるとき、
$$\begin{eqnarray}
&&f_2 - f_3 \\
&=& \psi(\alpha x_1 + \beta x_2 + c) - \psi(w_1h_1 + w_2h_2 + c)\\
&=& 0
\end{eqnarray}$$
が成り立ちます。ここで、出力層の活性化関数\(\psi\)が逆関数をもつとき、出力値が一意に決まると、活性化関数適用前の値も一意に決定するため、
$$
(\alpha x_1 + \beta x_2 + c) - (w_1h_1 + w_2h_2 + c) = 0
$$
という問題に置き換えることができます。
これから計算をしていきますが、説明を簡略化するために、\(b_1=b_2=0\)の場合を考えたいと思います。
$$\begin{eqnarray}
&&(\alpha x_1 + \beta x_2 + c) - (w_1h_1 + w_2h_2 + c) \\
&=& \alpha x_1 + \beta x_2 - w_1h_1 - w_2h_2 \\
&=& \alpha x_1 + \beta x_2 - w_1\phi(v_{11}x_1 + v_{21}x_2 + b_1) - w_2\phi(v_{12}x_1 + v_{22}x_2 + b_2) \\
&=& \alpha x_1 + \beta x_2 - w_1\phi(v_{11}x_1 + v_{21}x_2) - w_2\phi(v_{12}x_1 + v_{22}x_2)
\end{eqnarray}$$
これ以降の式変形の方針は、
$$
定数1 x_1 + 定数2 x_2
$$
という形に変更し、定数を0となるようにパラメータを調整することで、常に2つのニューラルネットが等価になることを説明することです。
そのためには、
$$\begin{eqnarray}
\phi(v_{11}x_1 + v_{21}x_2) &=& v_{11}\phi(x_1) + v_{21}\phi(x_2)\\
\phi(v_{12}x_1 + v_{22}x_2) &=& v_{12}\phi(x_1) + v_{22}\phi(x_2)
\end{eqnarray}$$
が成立する必要があります。これは、関数\(\phi\)が線形写像であるための必要十分条件です。よって、\(\phi(x) = Ax\)と書き換えると式変形の続きは
$$\begin{eqnarray}
&&\alpha x_1 + \beta x_2 - w_1\phi(v_{11}x_1 + v_{21}x_2) - w_2\phi(v_{12}x_1 + v_{22}x_2) \\
&=& \alpha x_1 + \beta x_2 - w_1v_{11}Ax_1 - w_1v_{21}Ax_2 - w_2v_{12}Ax_1 - w_2v_{22}Ax_2 \\
&=& (\alpha - w_1v_{11}A - w_2v_{12}A)x_1 + (\beta - w_2v_{21}A - w_1v_{22}A)x_2
\end{eqnarray}$$
となります。係数部分は
であり、パラメータを変更することで0にできます。これが何を示しているかというと、3層NNの中間層に線形関数を使用すると、その3層NNが得ることができる表現は、2層NNで完全に表すことができてしまうということです。すなわち表現能力が変わらないということです。
別の表現をするなら、ここまでの結論を使用して、中間層と出力層の活性化関数を線形関数(\(\phi(x) = Ax, \psi(x) = Bx\) ただし、\(A\)と\(B\)は定数)として3層NNの式に適用すると2層NNの式が導出できます。出力層の活性化関数も線形関数としておいたのは、線形関数は逆関数を持つからです。
output &=& \psi(w_1\phi(v_{11}x_1 + v_{21}x_2 + b_1) + w_2\phi(v_{12}x_1 + v_{22}x_2 + b_2) + c)\\
&=& ABw_1(v_{11}x_1 + v_{21}x_2 + b_1) + ABw_2(v_{12}x_1 + v_{22}x_2 + b_2) + Bc\\
&=& ABw_1v_{11}x_1 + ABw_1 v_{21}x_2 + ABw_1 b_1 + ABw_2v_{12}x_1 +ABw_2 v_{22}x_2 + ABw_2 b_2 + Bc\\
&=& AB(w_1v_{11} + w_2v_{12})x_1 + AB(w_1 v_{21} + w_2 v_{22})x_2 + B(Aw_1 b_1 + Aw_2 b_2 + c)\\
&=& \alpha x_1 + \beta x_2 + \gamma
\end{eqnarray}$$
よって、中間層の活性化関数に線形関数を使用すると、3層NNと2層NNが等価になることが分かります。より広くとらえれば、多層ニューラルネットワークがあったとき、中間層に線形関数を使用すると、使用した分だけ表現能力が低下、すなわち使用した層の存在意義が低下することが分かると思います。
まとめ
中間層のノードにおいて、活性化関数に線形関数を使用することは避けなければなりません。
