この記事ではGenerative Adversarial Networks(GANs)について解説していきます。
こんな方におすすめ
- GANについて詳しく知りたい
- GANのコードを動かしてみたい
では始めていきましょう!
GANとは
GANはGenerative Adversarial Networkの略で、日本語では、敵対的生成ネットワークと呼ばれます。2014年にイアングッドフェロー(Ian Goodfellow)らによって発表された機械学習フレームワークで、機械学習界隈に大きな革新を齎しました。
GANは学習によって、訓練データとして与えたデータに似たようなデータを生成することが可能で、一般的に生成モデルの一種とされます。
生成の具体例を見てみましょう。
[GANを使った画像生成の具体例を表した画像を入れる+画像の説明もいれる]
上記で示した画像の生成タスクの他、系列データにも適用が可能です。
GANは生成器と識別器から構成され、この2つのモデルを使用して敵対的な学習を行います。ここでは、敵対的な学習について簡単な紹介に留めますが、識別器は訓練データと生成器が生成したデータを見分けるように学習し、生成器は自身が生成したデータが識別機によってご認識、すなわち、訓練データと見間違うように学習します。これは損失関数のミニマックス問題に帰着させることが可能なことを後で紹介します。これが敵対的ネットワークにおける敵対的の意味であり、敵対的と呼ばれる所以です。
生成モデルと識別モデル
ここでは、GANを理解するうえで必要な知識である生成モデルと識別モデルについて紹介します。
生成モデル
生成モデルとは、手元にある実データが何らかの分布から生成されていると仮定して、生成器自身が持つ分布をそれに近づけることで獲得されるモデルです。ここでは仮に実データを生成している分布を\(p_d\)、生成モデルの持つ分布を\(p_g\)と置き、それらの分布の近さをはかる何らかの指標\(L\)により互いの分布の近さ定量的に計測し、\(L(p_d, p_g)\)を最小化する分布\(p_g\)を獲得します。すなわち、
$$
argmin_{p_g}L(p_d, p_g)
$$
が生成モデルの学習です。ここで、「なんらかの近さの指標」という表現をしていますが、どのような指標を使用するかにより獲得できる生成モデルの性能に差が出てきます。すこし先回りしてGANの生成モデルについて触れると、GANの生成モデルで使用する近さの指標はJSダイバージェンスと呼ばれるものです。詳細は後の章で説明します。
このように、生成モデルは実データの分布を近似するため、適切な分布が獲得できれば実際のデータと相違ないレベルのデータを無限に生成することが可能になります。
識別モデル
識別モデルとは、入力されたデータを正しくクラス分けすることができるモデルのことを言います。具体例を上げると、犬の写真と猫の写真を入力して、それらを犬クラスと猫クラスに分類するような問題を扱うモデルです。
ここでも、先回りしてGANの識別モデルについて触れると、GANの識別モデルでは犬や猫といった具体的なものの分類ではなく、確率分布の分類を行います。つまり、入力されたデータが実データを生成する分布から生成されたものなのか、生成器が持つ分布から生成されたデータなのかを分類するわけです。詳細は後の章で説明します。
生成モデルと識別モデルのまとめ
入力データを\(x\)、そのラベルを\(y\)として生成モデルと識別モデルが学習で近似するものを表にすると次のようになります。
| 分類モデル | モデル化対象 | 概要 |
|---|---|---|
| 生成モデル | \(P(x, y)\) or \(P(x)\) | データ\(x\)とラベル\(y\)の同時確率\(P(x, y)\)もしくはラベルがない場合はデータ\(x\)をモデル化 |
| 識別モデル | \(P(y|x)\) | 入力\(x\)からクラス\(y\)を直接モデル化 |
それぞれを図示すると以下のようになります。左が識別モデルの場合、右が生成モデルの場合を示しています。ここに、チューリップとひまわりの画像があるとします。これを綺麗に分割できるような境界を学習するのが識別器です。そのため、入力画像のラベルがチューリップなのか、ひまわりなのか、その確率を出力します。一方で、各々の画像とそのラベルが同時に生成する確率をモデル化するのが生成モデルです。右図の等高線のような分布を学習するイメージです。
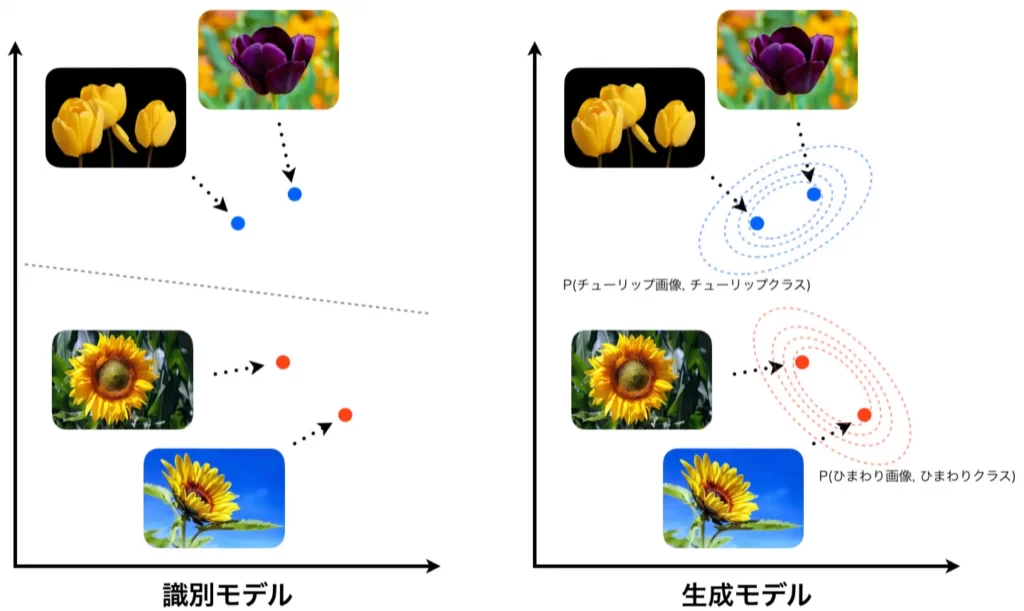
少々余談ですが、生成モデルは識別モデルとしても使用可能であることを以下に示します。
$$\begin{eqnarray}
\mbox{識別モデル} &=& P(y|x)\\
&=& \frac{P(x|y)P(y)}{P(x)}\\
&\propto& P(x|y)P(y)\\
\end{eqnarray}$$
上記の式変形で分母の\(x\)が消せる理由は、識別モデルというのは、\(x\)を固定して\(argmax_y P(y|x)\)を求めることでクラスラベルを予測することに起因し、生成モデルを使って識別する際は\(argmax_yP(x|y)P(y)\)で十分であるためです。
ここで注意点ですが、生成モデルから識別モデルを得ることができても、逆は成り立たないため識別モデルから生成モデルを得ることはできません。
GANが獲得する生成モデル
GANの学習においては、訓練データのクラスラベル(例えば、入力画像がチューリップなのかヒマワリなのか)を扱わないため、先ほどのような(下図左に再掲)チューリップの画像とチューリップクラスの同時確率を計算することはせず、チューリップの画像やヒマワリの画像すべてを混ぜた状態で、その訓練画像全体が1つの分布を構成しているとみなして生成モデルで近似します。
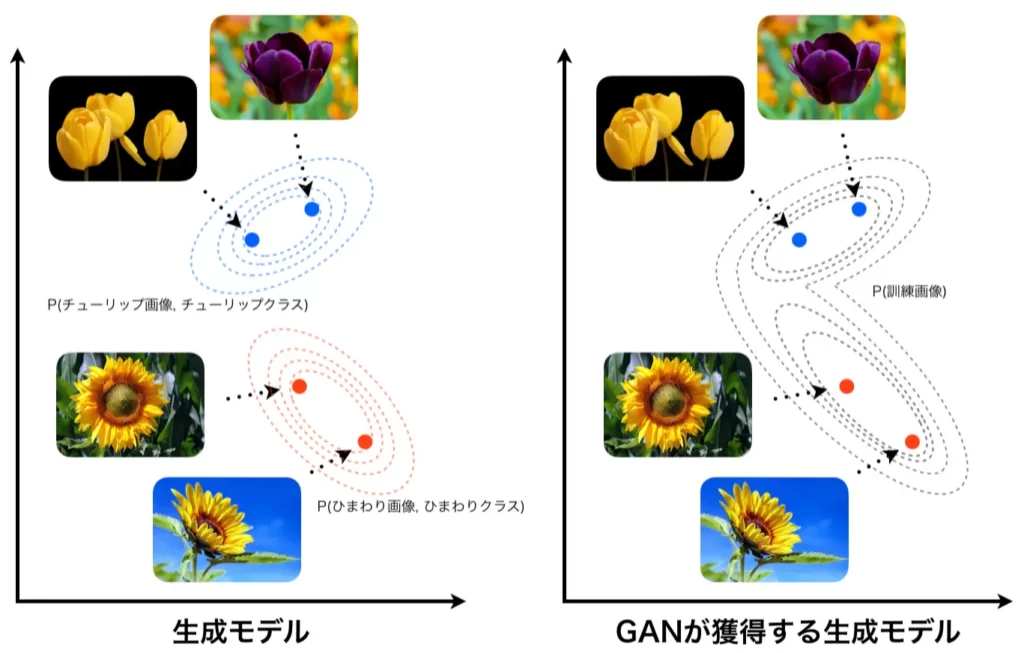
以降では、この訓練データの分布をデータ分布、GANの生成器が持つ分布をモデル分布と呼ぶことにし、それぞれ\(p_d\)、\(p_g\)と置くことにします。
GANのアーキテクチャ
GANのアーキテクチャについて解説していきますがその前に語句の定義をしておきたいと思います
| データ分布 | 訓練データを生成した背後にある分布 |
| モデル分布 | 生成器(生成モデル)が持つ分布 |
| データ空間 | データとして生成されうる空間のことでデータ分布やモデル分布からサンプリングされたデータ\(\in\)データ空間 |
GANの構成要素は生成器(生成モデル)と識別器(識別モデル)で、構成は以下に示すようになっています。
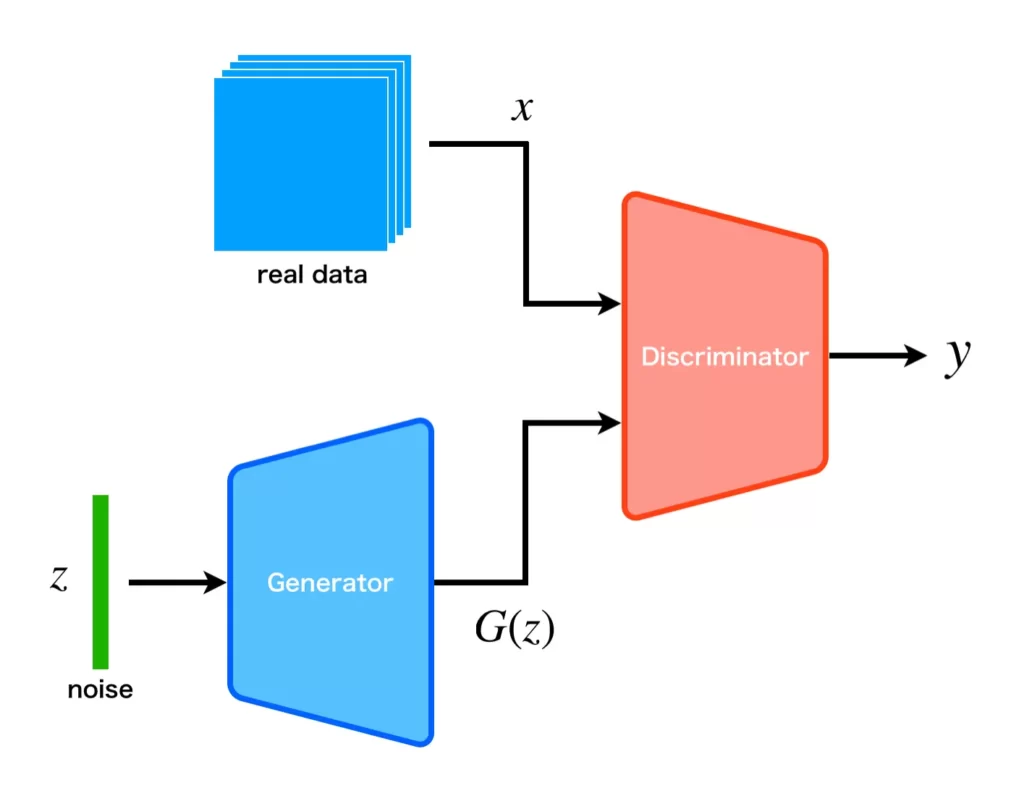
生成器は一様分布からサンプリングされたランダムノイズ\(\boldsymbol{z}\)に\(G(\boldsymbol{z})\in\mbox{データ空間}\)なる変換を施します。ランダムノイズを使用することで、モデル分布\(p_g(\boldsymbol{x})\)からサンプリングを実現しているわけです。そして、生成器から生成されたデータと訓練データ(実データ)は識別機に入力され、訓練データに属する確率[0, 1]が出力されます。
生成器は学習初期はデタラメなデータを出力するので、識別器も容易に真偽を学習することができます。徐々に学習が進むと、生成器は訓練データに近いデータを生成することが可能になり、識別器は真偽判定が困難になり、出力は1/2に近くなります。
このとき、モデル分布はデータ分布にかなり近い状態になっている、すなわち、データ分布を近似できていると考えることができます。
GANの損失関数
生成器を関数\(G\)、識別機を関数\(D\)、ノイズを\(\boldsymbol{z}\)、実データを\(\boldsymbol{x}\)、正解ラベルを\(\boldsymbol{y}\)と置きます。
最初に、モデル分布\(p_g\)からデータをサンプリングするプロセスを数式化します。生成器のパラメータ集合を\(\theta_g\)、ノイズ\(\boldsymbol{z} \mathtt{\sim} p_{\boldsymbol{z}}(\boldsymbol{z})\)とすると、生成モデルから生成されるデータは\(G(\boldsymbol{z}; \theta_g)\)と表せます。
次に、識別モデルによる識別プロセスを数式化します。識別モデルのパラメータを\(\theta_d\)、データ空間からサンプリングされたデータを\(\boldsymbol{x}\)とすると、データが訓練データに属する確率へのマッピング\(D(\boldsymbol{x}; \theta_d)\)と表せます。
データ\(\boldsymbol{x}\)に対する識別モデルへの教師信号(クラスラベル\(\boldsymbol{y}\))は、\(\boldsymbol{x}\)がデータ分布からサンプリングされたものなら1、モデル分布からサンプリングされたものなら0とします。これは2値分類問題であり、交差エントロピー(からマイナスを取り除いた式)で表すことができます。
$$
\sum_i\left\{y_i\log D(\boldsymbol{x_i}) + (1 – y_i)\log (1 – D(G(\boldsymbol{z_i})))\right\}
$$
ここで、識別器と生成器は以下の2ステップで学習をします。
- 識別器の学習:生成器を固定した状態で、データ分布とモデル分布を正しく識別できるように学習
- 生成器の学習:識別器を固定した状態で、識別器が生成器が生成したデータを誤識別するように学習
このとき、GANの誤差関数は以下のミニマックスゲームとして定式化することができます。
$$
\min_G \max_D V(D, G) = \displaystyle E_{\boldsymbol{x} \mathtt{\sim} p_d(\boldsymbol{x})}[\log D(\boldsymbol{x})] + \displaystyle E_{\boldsymbol{z} \mathtt{\sim} p_{\boldsymbol{z}}(\boldsymbol{z})}[\log (1 - D(G(\boldsymbol{z})))]
$$
- \(\displaystyle E_{\boldsymbol{x} \mathtt{\sim} p_d(\boldsymbol{x})}[\log D(\boldsymbol{x})]\):データ分布からサンプリングされたデータ\(\boldsymbol{x}\)についてDiscriminatorが出力した確率の対数の期待値。
- \(\displaystyle E_{\boldsymbol{z} \mathtt{\sim} p_{\boldsymbol{z}}(\boldsymbol{z})}[\log (1 - D(G(\boldsymbol{z})))]\):モデル分布からサンプリングされたデータについてDiscriminatorが出力した確率を1から引き対数を適用した値の期待値。
これでGANの損失関数の導出は終了ですが、実は、生成器の損失関数はもっと簡単にできることが分かると思います。式をよく見ると、第一項には生成器が含まれでいないので、第二項だけで十分なのです。ここまでの話を図にまとめると次のようになります。
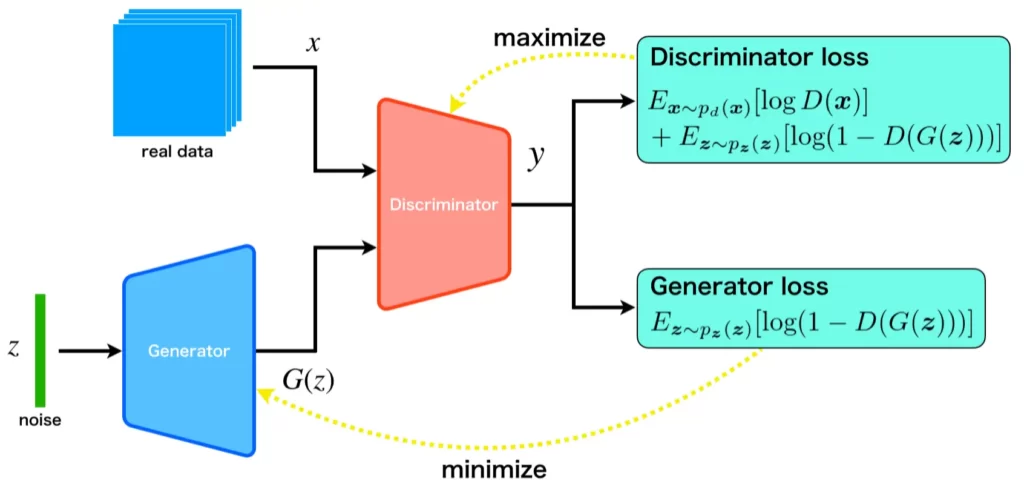
GANの損失関数の注意点
先ほど紹介したGANの損失関数
$$
V(D, G) = \displaystyle E_{\boldsymbol{x} \mathtt{\sim} p_d(\boldsymbol{x})}[\log D(\boldsymbol{x})] + \displaystyle E_{\boldsymbol{z} \mathtt{\sim} p_{\boldsymbol{z}}(\boldsymbol{z})}[\log (1 - D(G(\boldsymbol{z})))]
$$
は利用時に注意点があります。それは、データ分布及びモデル分布からサンプリングするデータ数の比率が等しいことを仮定している点です。
そのため、\(p_d\)からサンプリングしてきたデータ数を\(n_d\)、 \(p_g\)からサンプリングしてきたデータ数を\(n_g\)と置いたとき、
$$
n_d:n_g = 1:1
$$
ではない場合、以下のように損失関数の期待値に重みをかけて比率に応じて全体に与える影響を調節する必要があります。
$$
V(D, G) = \alpha\displaystyle E_{\boldsymbol{x} \mathtt{\sim} p_d(\boldsymbol{x})}[\log D(\boldsymbol{x})] + (1-\alpha) \displaystyle E_{\boldsymbol{z} \mathtt{\sim} p_{\boldsymbol{z}}(\boldsymbol{z})}[\log (1 - D(G(\boldsymbol{z})))]
$$
ここで、\(\alpha =\frac{n_d}{n_d+n_g}\)です。
これは、多くの場合問題にならないと思いますが、見落としがちなところなので注意したいところです。
GANの学習アルゴリズム
ここまでの内容でGANの損失関数について理解できたことと思います。しかし、これで本当に生成モデルが学習できるのか疑問に思われている方が多いと思いますので、その学習の流れ(アルゴリズム)についてイメージで理解できるように解説していきます。
GANの4つの学習状態
GANは未学習、識別器の学習、生成器の学習、収束状態の4つ状態があります。それぞれA,B,C,Dと置くことにします。
| A | 学習前のモデル分布\(p_g\)がデータ分布\(p_d\)と離れていて識別器はそれらを正しく識別できない(生成器・識別器ともに未学習)。 |
| B | 識別器の学習フェーズ。すなわち、与えられた\(p_g\)と\(p_d\)を識別する最適な\(D^*(\boldsymbol{x}) = \frac{p_d(\boldsymbol{x})}{p_d(\boldsymbol{x}) + p_g(\boldsymbol{x})}\)の獲得に向けて学習を実施。 |
| C | 生成器の学習フェーズ。すなわち、(B)の状態の識別器が誤識別するようにモデル分布を更新。 |
| D | BとCを何度も繰り返して、\(p_g=p_d\)となったときに学習を終了。このとき識別器の出力分布は0.5となる。ナッシュ均衡。 |
それぞれの状態におけるモデル分布\(p_g(\boldsymbol{x})\)(オレンジ)および識別器の出力分布\(D(\boldsymbol{x})\)(赤)を以下の図に示しました。
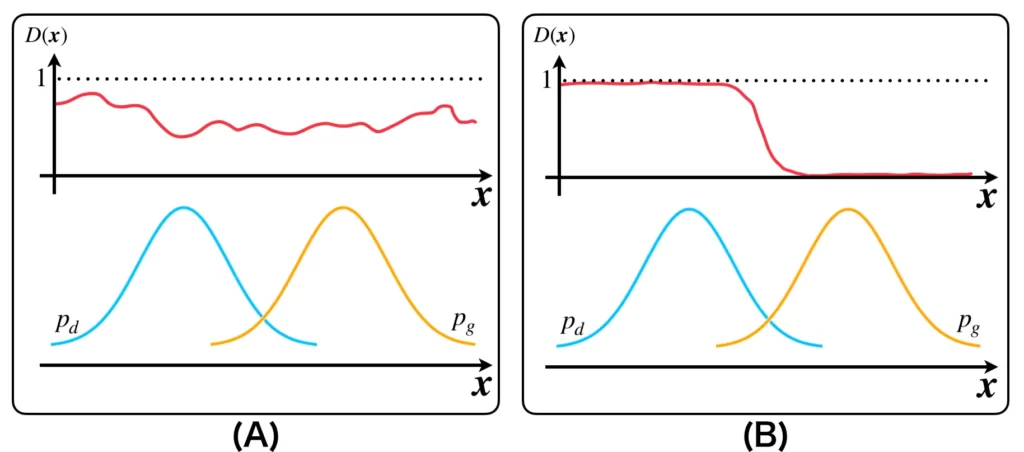
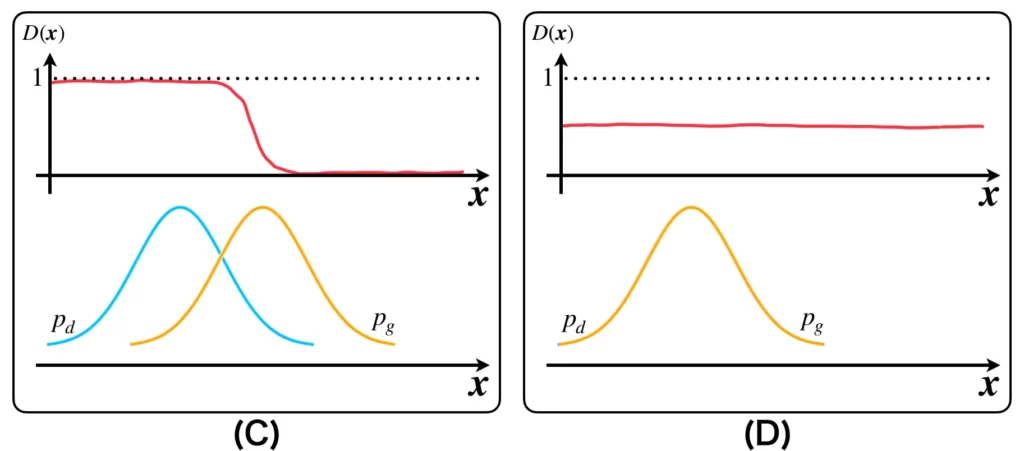
上図(A)は、データ分布とモデル分布が離れていて、識別器もそれぞれを識別できない状態Aを表しています。図(B)は識別器の学習によりデータ分布とモデル分布が識別できるようになった状態Bを表しています。図(C)は識別器が誤認識するように生成器を学習したことでモデル分布が更新された状態Cを表しています。図(D)は状態Bと状態Cを繰り返し行ったことで、モデル分布が完全にデータ分布に重なり、識別器の出力が1/2になった状態Dを表しています。
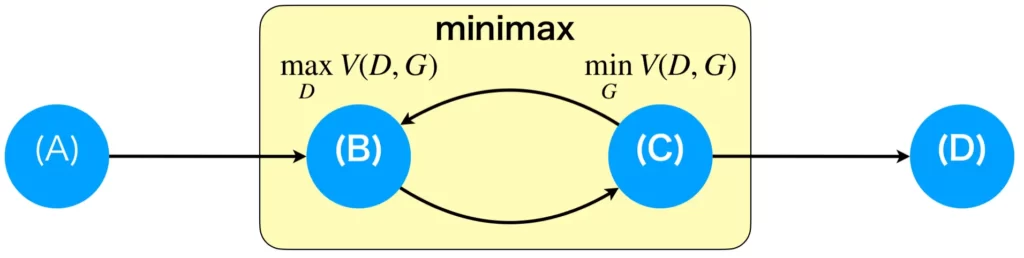
この4つの状態A,B,C,Dを状態遷移図で表すと次のようになります。注目してほしいのは、(B)と(C)が誤差関数のミニマックスゲームになっている点です。
学習アルゴリズム
ここでは学習アルゴリズムについて図を使用して一連の流れを説明します。
基本的なアルゴリズム
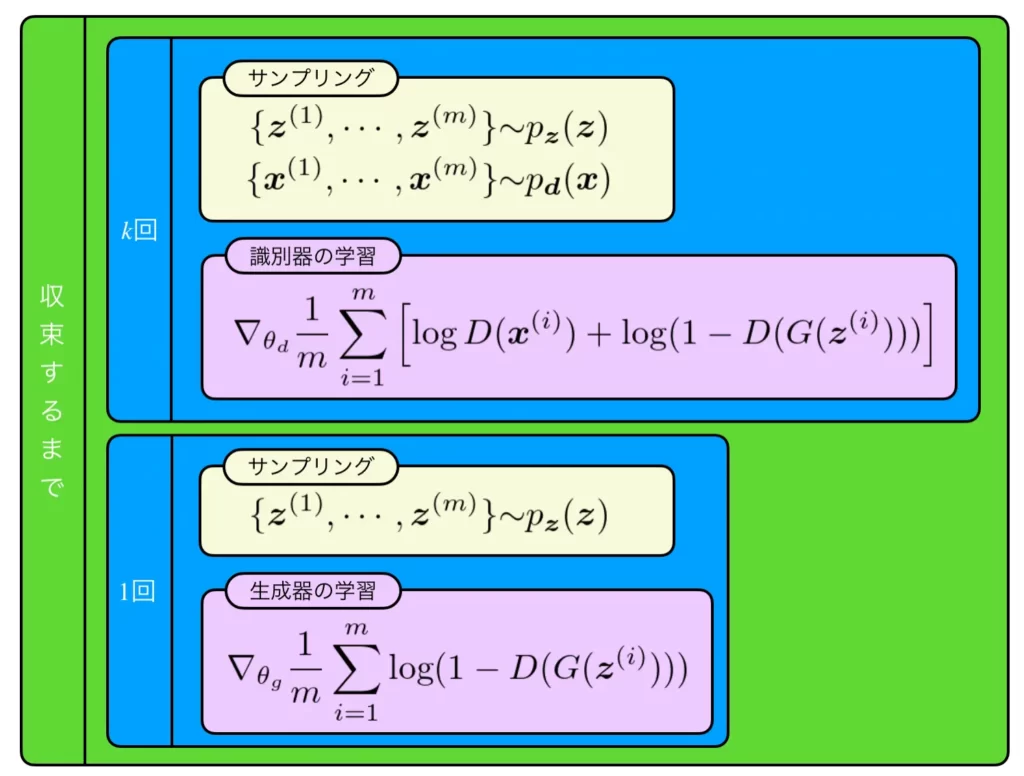
一通り流れを説明します。まず、識別器の学習を\(k\)回行います(ただし\(k=1\)とするのが一般的)。そこでは、生成器からデータを生成する際の種となるランダムベクトルを\(m\)個、実データから\(m\)個サンプリングしてきます。それらを使用して識別器の損失関数に代入し、勾配を求めます。あとは、その勾配を使用して識別器のパラメータ\(\theta_d\)を更新します。それが終わったら生成器の学習を行います。そこでは、生成器からデータを生成する際の種となるランダムベクトルを\(m\)個サンプリングして、生成器の損失関数に代入し、勾配を求めます。あとは、その勾配を使用して生成器のパラメータ\(\theta_g\)を更新します。これを識別器の出力が理想状態になるまで繰り返します。しかし、それは現実的ではないので、学習イテレーションを指定して、その回数分だけ実行します。
サンプリング数がデータ分布からとモデル分布からで異なる場合
基本的な学習アルゴリズムは上で紹介した通りですが、なんらかの理由でデータ分布からサンプリングしたデータ数とモデル分布からサンプリングしたデータ数が異なる場合、それぞれの個数を\(m\)および\(n\)として、以下のアルゴリズムにより学習を行います。
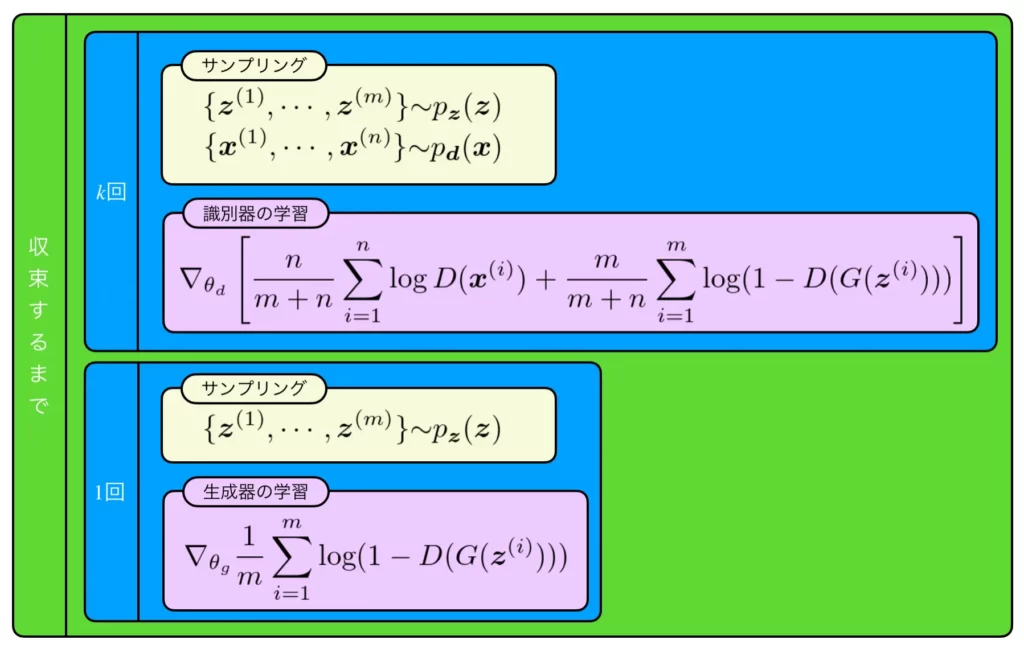
基本的なアルゴリズムとの違いは、識別器の損失関数内の各期待値にデータ数に応じた比率が重み付けされている点です。データ数の比率に偏りがある場合、これがないと、適切な最適化行われない可能性があるので注意してください。
ナッシュ均衡とGANの収束
ナッシュ均衡
ナッシュ均衡はゲーム理論の中でも非協力なゲーム戦略において、すべてのプレイヤーが自らの利益が最大となるような最適戦略をとっている状態のことです。この状態では、それぞれのプレイヤーはこれ以上戦略を変更する動機がなく均衡状態になっています。
GANの収束
GANにおいて、識別器と生成器をプレイヤーと考えると、以下のプレーを行っていると解釈できます。
- 識別器:自らの利益が最大(=損失関数が最大)になるように戦略(=重みパラメータ)を変更
- 生成器:自らの利益が最大(=損失関数が最小)になるように戦略(=重みパラメータ)を変更
それぞれが最適な状態では、モデル分布はデータ分布を完全に近似しているため、識別器の出力は1/2です。この状態では、生成器はこれ以上重みを変更する必要はなく、識別器もまた重みを変更する必要はありません。もし、ここで生成器が重みを変更したら、データ分布の最適な近似状態からズレてしまい、喪失関数の値が大きくなってしまいます。これは、利益が減少することを意味し、これ以上重みを更新する動機がないことが分かります。同様に、もし、ここで識別器が重みを更新したら、損失関数が最大の状態ではなくなってしまいます。よって、これ以上重みを更新する動機はありません。
このように、GANの収束状態はナッシュ均衡になります。
(とはいえ、実際の実装においてGANがナッシュ均衡に収束するのは難しく大抵は実現できないらしいが、もんだいないみたい)
GANの学習の問題点
ナッシュ均衡に収束せず振動する
mode collapse
データ分布がモデル分布で近似されるプロセス
生成器が近似するのはデータ分布です。しかし、GANの学習で、本当にモデル分布が近似できるのでしょうか?
この章では状態Cにおける最適化の数式を変換していくと、JSダイバージェンスによる表現が可能であることを示したいと思います。
※JSダイバージェンスについては後で説明します。
状態Cにおける最適化の式を求めるには、状態Bで得られると考えられる最適な識別器\(D^*_G\)(任意の生成器\(G\)に対して最適な\(D^*\)を表す)を求める必要があります。
最適な識別器(D)の導出
先ほど示した損失関数\(V(D, G)\)を式変形します。
$$\begin{eqnarray}
V(D, G) &=& \displaystyle E_{\boldsymbol{x} \mathtt{\sim} p_d(\boldsymbol{x})}[\log D(\boldsymbol{x})] + \displaystyle E_{\boldsymbol{z} \mathtt{\sim} p_{\boldsymbol{z}}(\boldsymbol{z})}[\log (1 - D(G(\boldsymbol{z})))]\\
&=& \displaystyle E_{\boldsymbol{x} \mathtt{\sim} p_d(\boldsymbol{x})}[\log D(\boldsymbol{x})] + \displaystyle E_{\boldsymbol{x} \mathtt{\sim} p_g(\boldsymbol{x})}[\log (1 - D(\boldsymbol{x}))]\\
&=& \int_\boldsymbol{x} \left\{ p_d(\boldsymbol{x})\log D(\boldsymbol{x}) + p_g(\boldsymbol{x})\log (1-D(\boldsymbol{x})) \right\} d\boldsymbol{x}
\end{eqnarray}$$
この式を最大にする最適な\(D^*_G\)を[0, 1]の制約の下で求めると、
$$
D^*_G = \frac{p_d(\boldsymbol{x})}{p_d(\boldsymbol{x}) + p_g(\boldsymbol{x})}
$$
となります。
状態Cにおける損失関数の導出
では、\(D^*_G\)を損失関数に代入し、\(V(D^*_G, G)\)を導出します。
$$\begin{eqnarray}
V(D^*_G, G) &=& \max_D V(D, G)\\
&=&\displaystyle E_{\boldsymbol{x} \mathtt{\sim} p_d(\boldsymbol{x})}[\log D^*_G(\boldsymbol{x})] + \displaystyle E_{\boldsymbol{x} \mathtt{\sim} p_g(\boldsymbol{x})}[\log (1 - D^*_G(\boldsymbol{x}))]\\
&=& \displaystyle E_{\boldsymbol{x} \mathtt{\sim} p_d(\boldsymbol{x})}\left[\log \left( \frac{p_d(\boldsymbol{x})}{p_d(\boldsymbol{x}) + p_g(\boldsymbol{x})} \right)\right] + \displaystyle E_{\boldsymbol{x} \mathtt{\sim} p_g(\boldsymbol{x})}\left[\log \left(1 - \frac{p_d(\boldsymbol{x})}{p_d(\boldsymbol{x}) + p_g(\boldsymbol{x})} \right)\right]\\
&=& \displaystyle E_{\boldsymbol{x} \mathtt{\sim} p_d(\boldsymbol{x})}\left[\log \left(\frac{p_d(\boldsymbol{x})}{p_d(\boldsymbol{x}) + p_g(\boldsymbol{x})} \right)\right] + \displaystyle E_{\boldsymbol{x} \mathtt{\sim} p_g(\boldsymbol{x})}\left[\log \left(\frac{p_g(\boldsymbol{x})}{p_d(\boldsymbol{x}) + p_g(\boldsymbol{x})} \right)\right]
\end{eqnarray}$$
導出自体はこれで終わりですが、我々が仕組みを理解する上ではまだ不十分ですので、もっと式変形を行っていきます。以下は上の式変形の続きです。既に式変形の方針が決まっていて、強引な部分もあり、天下り的ですがご容赦ください。
$$\begin{eqnarray}
V(D^*_G, G) &=& \displaystyle E_{\boldsymbol{x} \mathtt{\sim} p_d(\boldsymbol{x})}\left[\log \left(\frac{p_d(\boldsymbol{x})}{p_d(\boldsymbol{x}) + p_g(\boldsymbol{x})} \right)\right] + \displaystyle E_{\boldsymbol{x} \mathtt{\sim} p_g(\boldsymbol{x})}\left[\log \left(\frac{p_g(\boldsymbol{x})}{p_d(\boldsymbol{x}) + p_g(\boldsymbol{x})} \right)\right]\\
&=& - \log 4 + \log 4 + \displaystyle E_{\boldsymbol{x} \mathtt{\sim} p_d(\boldsymbol{x})}\left[\log \left(\frac{p_d(\boldsymbol{x})}{p_d(\boldsymbol{x}) + p_g(\boldsymbol{x})} \right)\right] + \displaystyle E_{\boldsymbol{x} \mathtt{\sim} p_g(\boldsymbol{x})}\left[\log \left(\frac{p_g(\boldsymbol{x})}{p_d(\boldsymbol{x}) + p_g(\boldsymbol{x})} \right)\right]\\
&=& - \log 4 + \displaystyle E_{\boldsymbol{x} \mathtt{\sim} p_d(\boldsymbol{x})}\left[\log \left(\frac{2p_d(\boldsymbol{x})}{p_d(\boldsymbol{x}) + p_g(\boldsymbol{x})} \right)\right] + \displaystyle E_{\boldsymbol{x} \mathtt{\sim} p_g(\boldsymbol{x})}\left[\log \left(\frac{2p_g(\boldsymbol{x})}{p_d(\boldsymbol{x}) + p_g(\boldsymbol{x})} \right)\right]\\
&=& - \log 4 + \displaystyle E_{\boldsymbol{x} \mathtt{\sim} p_d(\boldsymbol{x})}\left[\log \left(\frac{p_d(\boldsymbol{x})}{\frac{p_d(\boldsymbol{x}) + p_g(\boldsymbol{x})}{2}} \right)\right] + \displaystyle E_{\boldsymbol{x} \mathtt{\sim} p_g(\boldsymbol{x})}\left[\log \left(\frac{p_g(\boldsymbol{x})}{\frac{p_d(\boldsymbol{x}) + p_g(\boldsymbol{x})}{2}} \right)\right]\\
&=& - \log 4 + D_{KL}\left(p_d(\boldsymbol{x}) \middle|\middle| \frac{p_d(\boldsymbol{x}) + p_g(\boldsymbol{x})}{2} \right) + D_{KL} \left(p_g(\boldsymbol{x}) \middle|\middle| \frac{p_d(\boldsymbol{x}) + p_g(\boldsymbol{x})}{2} \right)\\
&=& - \log 4 + 2\left\{\frac{1}{2}D_{KL}\left(p_d(\boldsymbol{x}) \middle|\middle| \frac{p_d(\boldsymbol{x}) + p_g(\boldsymbol{x})}{2} \right) + \frac{1}{2}D_{KL} \left(p_g(\boldsymbol{x}) \middle|\middle| \frac{p_d(\boldsymbol{x}) + p_g(\boldsymbol{x})}{2} \right)\right\}\\
&=& - \log 4 + 2D_{JS}\left(p_d(\boldsymbol{x}) \middle|\middle| p_g(\boldsymbol{x}) \right)
\end{eqnarray}$$
とても長い式変形になりましたが、最終的にはJSダイバージェンス(Jensen-Shannon divergence)による式で表せました。JSダイバージェンスとは、二つの分布(ここでは、\(p_d\)と\(p_g\))の近さを表し、それらが等しいとき(\(p_g=p_d\))に値が0になります。その他、JSダイバージェンスの詳しい解説はここでは省略します。
ここから、状態Cにおいて、生成器を学習する際は、JSダイバージェンスの値が小さくなるように、即ち、モデル分布\(p_g\)がデータ分布\(p_d\)に近づくように学習されることがご理解いただけると思います。
補足
本記事の初めに生成モデルについて解説しましたが、そこでは生成モデルとはデータ分布とモデル分布間の近さをはかる何らかの指標を最小化することで得られると説明しました。その指標がJSダイバージェンスなわけですが、GANの損失関数からは、ぱっと見ただけではJSダイバージェンスの影も形も無いため、疑問に思われた方もいるかもしれません。そこで、上の「状態Cにおける損失関数の導出」では、GANの損失関数からJSダイバージェンスが導出できることを証明しました。よって、GANの損失関数とJSダイバージェンスは等価なのです。
GANのライブラリ
GANをプログラミングする際に使用するライブラリと聞くと、何を思い浮かべるでしょか?TensorFlowやPyTorchでしょうか?
もちろん、これらを使ってGANプログラムを作成することも可能です。むしろ、ネットワークのアーキテクチャをしっかり理解する際には必要でしょう。しかし、ネットワークアーキテクチャを理解していないと難しいです。そこで、今回は、GANを簡単に扱うことを目的として作成されたライブラリやフレームワークを紹介したいと思います。
TF-GAN
TF-GANはGANを手軽に学習・評価するためのTensorFlowベースのライブラリです。TF-GANは複数の要素から構成されていて、それぞれが依存しないように設計されています。
vegans
vegansは様々な既存のGANや他の生成モデルを簡単に学習させるためのPyTorchベースのライブラリです。
最後に
本記事は、GANについて基礎から解説してきました。GANというと聞いたことがあっても、自分でプログラミングするのは大変そうなイメージを持つ人が多いでしょう。本記事を通じで、少しでも自分でやれるかもと感じていただけたら幸いです。最後までお読みいただきありがとうございますた。
