本日は、以降の記事で扱う深層学習で頻繁に表れる重要な概念であるKLダイバージェンス(KL情報量、相対エントロピーともいう)について扱いたいと思います。KLダイバージェンスの説明をするにあたり、情報理論の基礎から要点をまとめていきたいと思います。
(解説動画は作成中です。)
自己情報量
自己情報量とは情報理論において最も基礎をなす重要な概念で、ある事象が生起したときにどのくらいの情報を得るのかを確率をつかって定式化したものです。天下り的に結果を示すと、情報量\(I(x)\)は
$$
I(x) = \log\frac{1}{p(x)} = -\log p(x)
$$
のように表されます。なぜ対数が使用されているかですが、適当に決まったのではなく、得る情報量の連続性や加法性などといった情報を知るとはどういうことかの仮定に基づいて導出されたものです。自己情報量のグラフは以下のようになります。
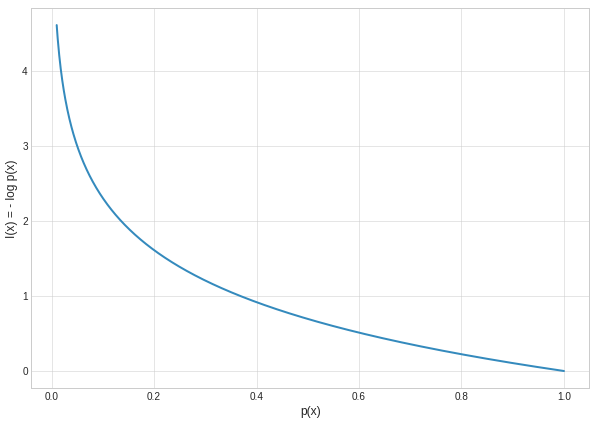
グラフから、生起する確率が小さい事象が生起したときは大きな情報を得られることを、高確率で生起する事象に関しては得られる情報が少ないことを示しています。つまり、低確率で生起する事象についてはたいてい知らないので生起したときは驚きますし、逆に高確率で生起する事象についてはたいてい知っているので生起したとしても関心が向くことはないでしょう。こういう意味で、確率から得られる情報をうまく定式化していることが分かります。
エントロピー
先ほど考えた情報量は、事象\(x\)についての生起確率に対して決められました。少し言い換えれば、ある集合\(\mathcal{X}\)があったとき、そこから事象\(x\)が生起(\(x\in\mathcal{X}\))するときの確率を使って自己情報量を定式化したわけです。少し拡張して考えると事象\(x\)についての情報量だけではなく、\(x\)が属する集合\(\mathcal{X}\)が従う確率分布について期待される情報量を考えることができるはずです。これがエントロピー\(H\)です。
$$\begin{eqnarray}
H(p(x)) & = & \mathbb{E}_{p(x)}[I(x)] = \mathbb{E}_{p(x)}[-\log p(x)]\\
(離散確率分布なら) H(p) & = & \sum_{x\in\mathcal{X}}p(x)(-\log p(x))\\
(連続確率分布なら) H(p) & = & \int_{-\infty}^{\infty}p(x)(-\log p(x))dx
\end{eqnarray}$$
エントロピーは確率分布で値が決定します。期待値を考えることで単独での情報量ではなく、情報量の平均を表すようになりました。よって、エントロピーはどの事象が生起するか予想することを考えたとき、その予想のしにくさ(事象の不確実性さ)を表していると解釈できます。この平均が最も高い確率分布は一様分布の時になります。以下に、エントロピーのグラフの例として2値エントロピー関数のグラフを示します。
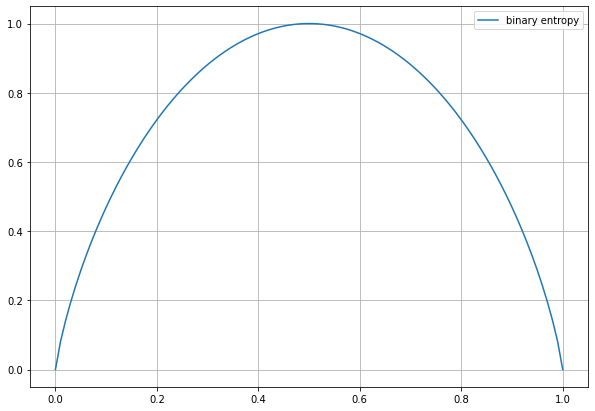
交差エントロピー
交差エントロピーは上で述べたエントロピーを拡張したものです。新たな確率分布\(q(x)\)を用意して、
$$\begin{eqnarray}
H(p(x), q(x)) & = & \mathbb{E}_{p(x)}[-\log q(x)]\\
(離散確率分布なら) H(p,q) & = & \sum_{x\in\mathcal{X}}p(x)(-\log q(x))\\
(連続確率分布なら) H(p,q) & = & \int_{-\infty}^{\infty}p(x)(-\log q(x))dx
\end{eqnarray}$$
確率\(q(x)\)の自己情報量が、確率\(p(x)\)で生起すると考えた時の期待値で書かれます。表記が同時エントロピーと同じなところは注意が必要です。
交差エントロピーの特別な場合、つまり\(q(x) = p(x)\)のとき、エントロピーと等しくなり、
$$
H(p(x), p(x)) = H(p(x))
$$
となります。
KLダイバージェンス(相対エントロピー)
エントロピーは確率分布に対して求まるものであることは理解できたと思います。先ほど定義した交差エントロピー\(H(p, q)\)とエントロピー\(H(p)\)では両方とも確率分布\(p\)に従うと仮定して期待値を求めました(\(\mathbb{E}_p[・]\))。このとき、2つの差を計算してみたくなりませんか?
2つの差を計算すると、確率分布\(p(x)\)と\(q(x)\)が似ているかどうか計算できます。これが相対エントロピー、機械学習においてKLダイバージェンスといわれるものです。
$$\begin{eqnarray}
KL(p(x)||q(x)) & = & H(p(x), q(x)) - H(p(x))\\
&=& \mathbb{E}_{p(x)}[-\log q(x)] - \mathbb{E}_{p(x)}[-\log p(x)]\\
&=& \mathbb{E}_{p(x)}[-\log q(x) + \log p(x)]\\
&=& \mathbb{E}_{p(x)}\left[\log\left(\frac{p(x)}{q(x)}\right)\right]\\
(離散確率分布なら) KL(p||q) & = & \sum_{x\in\mathcal{X}}p(x)log\left(\frac{p(x)}{q(x)}\right)\\
(連続確率分布なら) KL(p||q) & = & \int_{-\infty}^{\infty}p(x)log\left(\frac{p(x)}{q(x)}\right)dx
\end{eqnarray}$$
のように計算されます。ただし、注意点があり、\(KL(p||q) \neq KL(q||p)\)であり可換ではないため距離の公理を満たしません。そのため、KLダイバージェンスが表す似ているかどうかの尺度は距離ではありません。
KLダイバージェンスと最尤推定の関係
最尤推定とは、簡単に言うと事象\(x\)が真の確率分布\(p(x)\)に従って生起していると仮定したとき、真の確率分布\(p(x)\)は分からないので、\(p(x|\theta)\)で近似することができる\(\theta\)を推定する方法で、以下の対数尤度を最大化させる問題に帰着させます。
$$
\log L(\theta) = \sum_n^N\log p(x_n|\theta)
$$
$$
\max_\theta \log L(\theta)
$$
です。では、KLダイバージェンスを思い出してみましょう。\(KL(p(x)||p(x|\theta))\)を考えると、
$$\begin{eqnarray}
KL(p(x)||p(x|\theta)) &=& \sum_n p(x_n)\frac{p(x_n)}{p(x_n|\theta)}\\
&=& \sum_n p(x_n)\{\log p(x_n) - \log p(x_n|\theta)\}
\end{eqnarray}$$
となり、
$$
\min_\theta KL(p(x)||p(x|\theta))
$$
は、\(\log p(x_n) - \log p(x_n|\theta)\simeq0\)となることであり、未知の真の確率分布\(p(x)\)を推定することになります。
すなち、最尤推定とKLダイバージェンスの最小化は等価です。
KLダイバージェンスの使用例
KLダイバージェンスの使用例を1つとして、ニューロン発火のスパース化です。この内容は近々扱うスパースオートエンコーダの話と被りますが、ここでは、機械学習の話というよりはKLダイバージェンスの話に重きを置きたいので、機械学習用語は極力使用せずに説明したいとおもいます。
コインAとBを使ったコイン投げをすることを考えます。コインAは表が出る確率が\(P(X=表)=p\)、裏が出る確率が\(P(X=裏)=1-p\)、コインBは表が出る確率が\(Q(X=表)=q\)、裏が出る確率が\(Q(X=裏)=1-q\)とします。このとき、これら2つのベルヌーイ分布間の近さをKLダイバージェンスで表してみたいと思います。
$$\begin{eqnarray}
KL(P||Q)&=&\sum_{X\in\{表,裏\}}P(X)\log\frac{P(X)}{Q(X)}\\
&=&P(表)\log\frac{P(表)}{Q(表)}+P(裏)\log\frac{P(裏)}{Q(裏)}\\
&=&p\log\left(\frac{p}{q}\right) + (1-p)\log\left(\frac{1-p}{1-q}\right)
\end{eqnarray}$$
このとき、コインAを投げたときに表が出る確率\(p\)を0.2, 0.3, 0.5, 0.7と固定したとき、コインBを投げたときに表が出る確率\(q\)を\(0<q<1\)で変化させたときにグラフを以下に示します。]
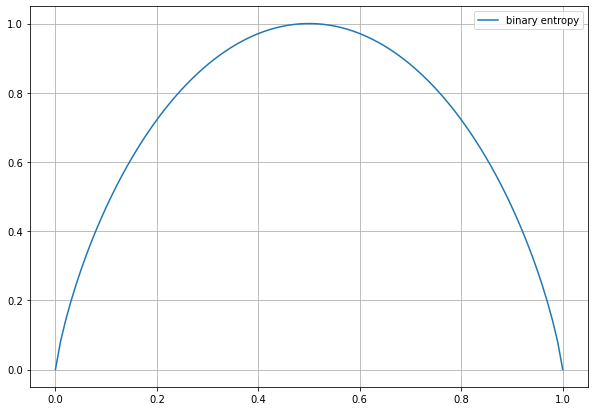
図から\(q=p\)となるときに最小値0をとること、\(p=0.5\)の場合を除き0の位置を中心としてグラフの形は対称にならないことが分かります。これにより、2つのベルヌーイ分布間の近さが図れることがご理解いただけたと思います。
要約
KLダイバージェンスは情報理論からのアプローチで導くことができ、2つの確率分布間の近さをエントロピーの考え方の元に定式化したものです。同じ確率分布のとき最小値0をとり、少しでも合致しない場合、正の数を返します。また、最尤推定と等価な働きを実現させることができます。ただし、引数が可換ではないところは注意が必要です。
今回の内容は以上になります。明日の記事は正則化とノルムについて扱う予定です。
