オートエンコーダ(autoencoder:AE)とは、教師なしでデータの特徴を学習することができるニューラルネットワークです。制約の手法を変えることでオートエンコーダはさまざまな特徴を学習することができます。オートエンコーダ入門Ⅰ回目では、オートエンコーダの専門的内容というよりは、基礎的な内容、特にオートエンコーダの構造的な分類、線形オートエンコーダ、不完備線形オートエンコーダと主成分分析、重み共有について紹介していきたいと思います。
大きなプログラムは扱いませんが、Google ColaboratoryのGistがありますのでご利用ください。
オートエンコーダの基本形
今後、さまざまなオートエンコーダを扱っていきますが、それらには基本形があります。よって、このセクションではオートエンコーダの基本形を示し定式化し、説明していきたいと思います。
オートエンコーダのフォワード計算の定式化
オートエンコーダとは、以下の図に示すような入力層、隠れ層、出力層からなる3層のニューラルネットワークのことをいます。より深層なオートエンコーダはスタックオートエンコーダ(stacked autoencoder:SAE)とよばれ、これらすべてを含めオートエンコーダと呼ばれますが、オートエンコーダの基本形は以下の3層ニューラルネットワークに帰着させて考えることができます。
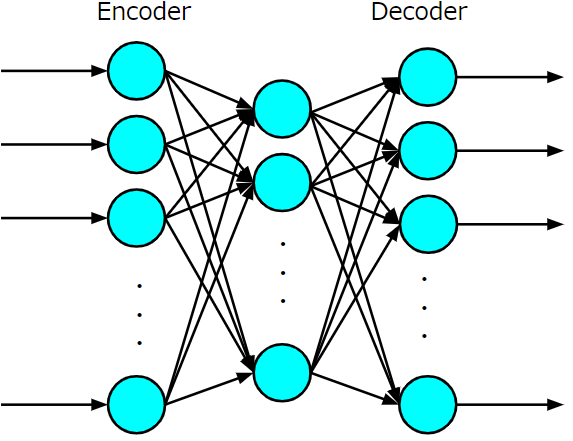
入力層から中間層にかけてをエンコーダ、中間層から出力層にかけてをデコーダといいます。また、中間層で得られる表現を内部表現といいます。オートエンコーダで注目したいのはエンコーダ部分の学習により得られる内部表現であり、その内部表現が適切なものになるように表現を獲得するのがオートエンコーダの使命となります。
では、以下の図のように入力、出力、重み、バイアス、活性化関数をおき、オートエンコーダを定式化します。
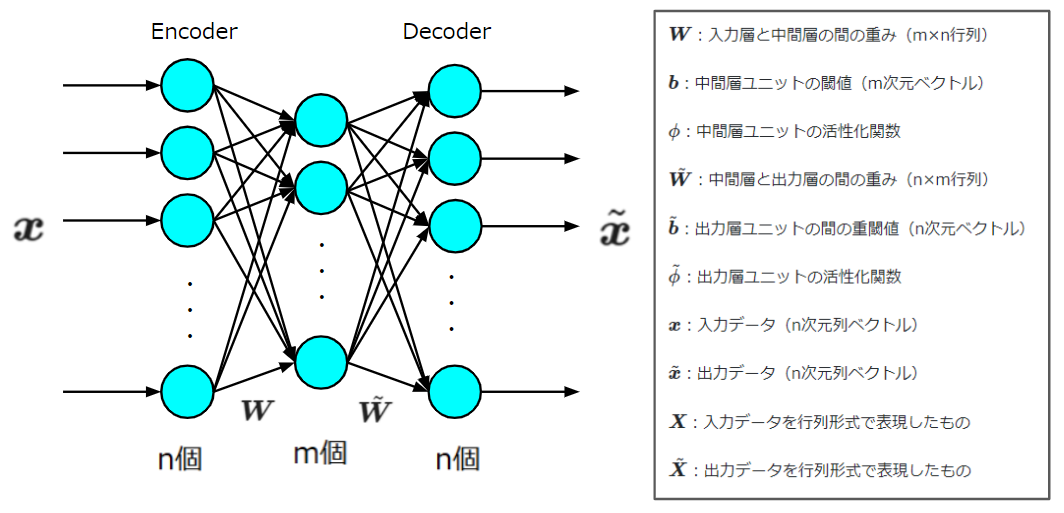
このような文字で置いたとき、出力は
$$\tilde{\boldsymbol{x}}=\tilde{\phi}(\tilde{\boldsymbol{W}}\phi(\boldsymbol{W}\boldsymbol{x}+\boldsymbol{b})+\tilde{\boldsymbol{b}})$$
と表現することができます。これはオートエンコーダの数式を一般化したもので、以降の説明では、この式に制約を設けたものを考えていくことになります。
ここで、
$$\phi(\boldsymbol{W}\boldsymbol{x}+\boldsymbol{b})$$
が内部表現になります。
オートエンコーダの学習(バックワード計算)
オートエンコーダの学習では誤差逆伝播法を使用した誤差関数の最適化によりおこないます。誤差関数として二乗誤差関数や交差エントロピー関数などを考えることができます。よって、例えば二乗誤差関数であれば、
$$L = \sum_i||\boldsymbol{x}_i - \tilde{\boldsymbol{x}}_i||^2 = \sum_i||\boldsymbol{x}_i - \tilde{\boldsymbol{W}}(\boldsymbol{W}\boldsymbol{x}+\boldsymbol{b})-\tilde{\boldsymbol{b}}||^2$$
を目的関数として定めることになります。追々説明しますがこれも基本形であり、スパース性制約を付加する場合は正則化項を付与します(オートエンコーダに限った考え方ではありません)。あと、誤差逆伝播に関する説明はここでは省略します。
オートエンコーダの分類
ここでは以降でオートエンコーダの性質を理解しやすいように、中間層のニューロン数による分類と、使用する活性化関数の種類による分類を説明します。これは私たちがハイパーパラメータとして与える部分、すなわち構造上の違いによる分類になります。もちろん、それ以外の分類方法もありますが、オートエンコーダの基礎的概念を理解するには十分です。
中間層のニューロン数による分類
オートエンコーダの中間層のニューロン数は、どのような内部表現を学習できるかの大きな指標の1つです。そこで、オートエンコーダの中間層のニューロン数を\(m\)、入&出力層のニューロン数を\(n\)とおいて、次の3パターンの関係を考えることにします。
- \(m<n\)
- \(m=n\)
- \(m>n\)
このとき、1番目の\(m<n\)な状態は中間層のニューロン数が入力層や出力層のニューロン数より少ないため、不完備なオートエンコーダといわれます。2番目の\(m=n\)は中間層のニューロン数が入力層や出力層のニューロン数と等しいため、完備なオートエンコーダといわれます。3番目の\(m>n\)は中間層のニューロン数が入力層や出力層のニューロン数より多いため、過完備なオートエンコーダといわれます。これらを図示すると以下のようになります。
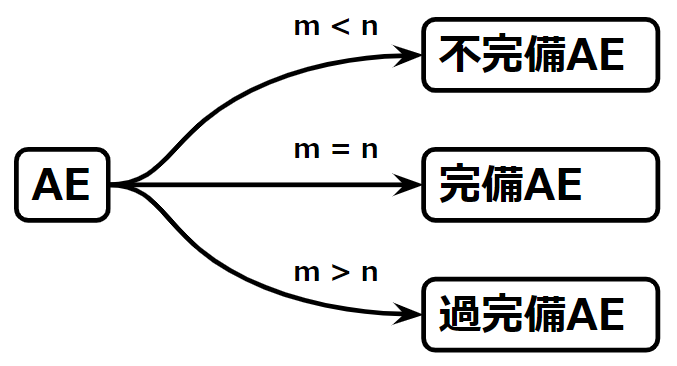
不完備なオートエンコーダでは内部表現の表現能力が入力データの表現能力より低いため、必然的に重要度の高い情報のみを学習することになりますが、完備、過完備なオートエンコーダでは、内部表現の表現能力が入力データの表現能力と同じか、それより高いため内部表現の学習には注意が必要になります。すなわち、恒等関数を学習できてしまうということです。そこで、ドロップアウトにより活性化するニューロン数を減らしたり、正則化によりスパース性制約を設けたりすることになります。
使用する活性化関数による分類
つぎは、使用する活性化関数の違いによる分類をしたいと思います。といってもそこまで難しくはありません。使用する活性化関数が線形なのか非線形なのかの2種類に大別されるだけです。
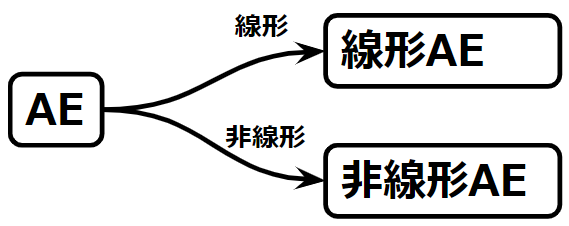
線形活性化関数を使用したオートエンコーダを線形オートエンコーダ、非線形活性化関数を使用したオートエンコーダを非線形オートエンコーダといいます。
分類のまとめ
いま説明した2つの分類方法を合体させると、オートエンコーダをより体系的に理解することができるようになります。以下の図を見てください。オートエンコーダは中間層のニューロン数の違いで不完備、完備、過完備に分類でき、さらに使用する活性化関数により、不完備線形オートエンコーダ、不完備非線形オートエンコーダ、完備線形オートエンコーダ、完備非線形オートエンコーダ、過完備線形オートエンコーダ、過完備非線形オートエンコーダに分類できることを示しています。
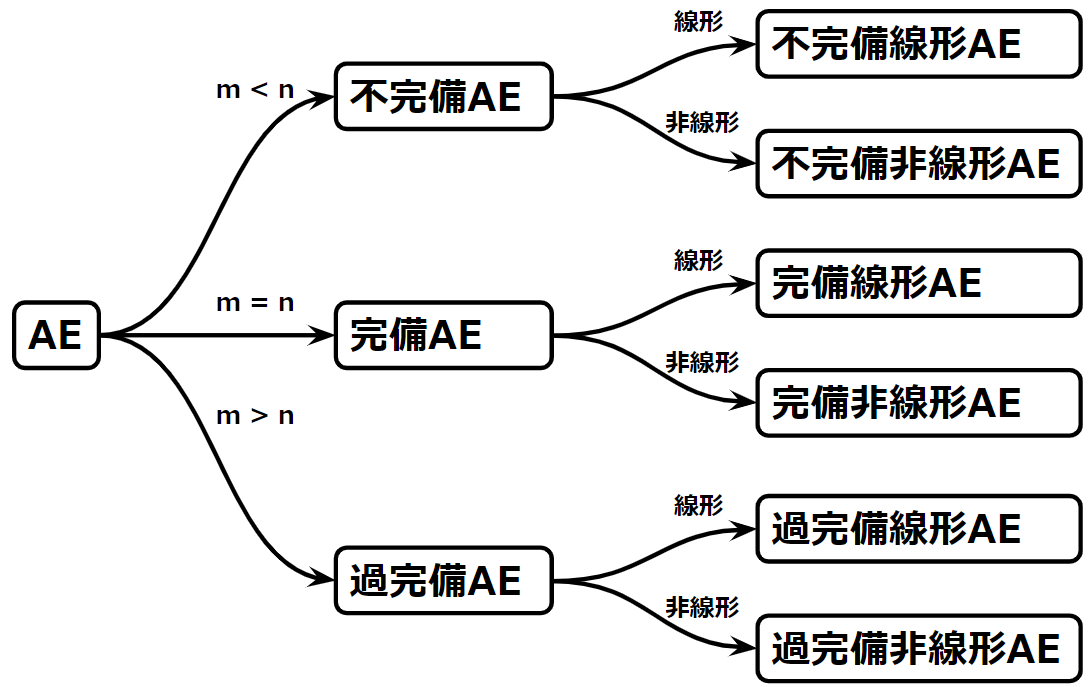
このように6分類できたので、PCAとの関係、スパース性制約の必要性等、理解しやすくする準備が整いました。
オートエンコーダ入門Ⅰでは、線形オートエンコーダに注目して説明を進めていきます。
線形オートエンコーダについて
以下では、目的関数に二乗誤差関数を採用することを前提としてそれぞれの線形オートエンコーダの性質について説明していきたいと思います。
完備・過完備線形オートエンコーダと恒等関数
オートエンコーダのなかで、完備線形オートエンコーダと過完備線形オートエンコーダは、恒等関数を学習することができます。できますといっても、喜ばしいことではありません。入力データのノイズも含めて学習してしまうためです。汎化性能を向上させるには、必要な情報と不必要な情報を選別し、次元の小さい上位概念を学習する必要があります。活性化関数が非線形なら話は別ですが(非線形活性化関数でも、線形で近似できる範囲にニューロンの計算が収まってしまう場合は注意)、線形な場合は、恒等関数、重みベクトルの点で見れば単位行列を学習しているにすぎません。式を見れば一目瞭然です。
$$\tilde{\boldsymbol{x}}=\tilde{\phi}(\tilde{\boldsymbol{W}}\phi(\boldsymbol{W}\boldsymbol{x}+\boldsymbol{b})+\tilde{\boldsymbol{b}})$$
において、活性化関数が傾き1の恒等関数であれば、
$$\begin{array}{rcl}
\tilde{\boldsymbol{x}}&=&\tilde{\boldsymbol{W}}(\boldsymbol{W}\boldsymbol{x}+\boldsymbol{b})+\tilde{\boldsymbol{b}}\\
&=&\tilde{\boldsymbol{W}}\boldsymbol{W}\boldsymbol{x}+\tilde{\boldsymbol{W}}\boldsymbol{b}+\tilde{\boldsymbol{b}}
\end{array}$$
ここで、\(\tilde{\boldsymbol{W}}\boldsymbol{W}=\boldsymbol{E}\)、\(\tilde{\boldsymbol{W}}\boldsymbol{b}+\tilde{\boldsymbol{b}}=\boldsymbol{0}\)とすれば、\(\tilde{\boldsymbol{x}}=\boldsymbol{x}\)です。完備、過完備では、中間層のニューロン数の関係が\(m \geq n\)なので、ランクを\(n\)より落とすことなく線形変換することが可能な表現を実現することができます。
このように、\(\tilde{\boldsymbol{x}}=\boldsymbol{x}\)が可能ということはノイズまで学習してしまうことを示しており、この場合、二乗誤差関数は最小値0となります。訓練データに対してだけでなくテストデータで性能を確かめるときにも高得点をだします(単位行列\(\tilde{\boldsymbol{W}}\boldsymbol{W}=\boldsymbol{E}\)で写像しているだけなので)ので過学習というのか迷いますが、どのみち内部表現が価値のあるものである可能性は低いです。
不完備線形オートエンコーダと主成分分析の関係
突然ですが、主成分分析(principal component analysis:PCA)とは何でしょうか。主成分分析とは分散共分散行列の固有ベクトルを求めて、そこから固有値の大きい固有ベクトルを選んできて、本質的な特徴をもつ次元の小さい空間の表現を求める際に使用されるアルゴリズムです。不完備線形オートエンコーダを使用すれば主成分分析で得られる内部表現を学習により獲得することができます。
不完備であれは、恒等関数をそのまま学習することはできません。そのかわり、恒等関数の近似を学習することになります。恒等関数を可能な範囲で最大限近似するためには、重要な特徴を残し、重要でない特徴は削る必要があることは容易に想像することができると思います。
実際にアヤメのデータを使用して不完備線形オートエンコーダと主成分分析が等価であることを確かめたいと思います。
アヤメのデータによる比較
まず、アヤメのデータを読み込みます。
# アヤメのデータを読み込む
from sklearn.datasets import load_iris
iris_data = load_iris()
# 学習用のデータを抽出
data = iris_data.data どのようなデータか簡単に説明すると、アヤメのデータセットとはsetosa、versicolor、virginicaの3種類について、花弁の長さと幅、がくの長さと幅という4つの属性もつものです。以下のコードを実行すると確認することができます。
# データを覗いてみる
import pandas as pd
df = pd.DataFrame(data, columns=iris_data.feature_names)
df.head()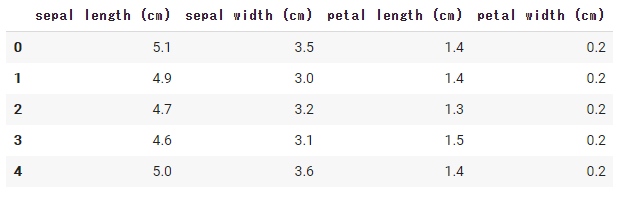
このままでは特徴のスケールが異なるので、標準化したいと思います。
from sklearn.preprocessing import StandardScaler
sscaler = StandardScaler()
data_sc = sscaler.fit_transform(data)
# data_sc.mean(axis=0) # ほぼ0
# data_sc.std(axis=0) # ほぼ1興味がある方は、標準化後のデータを覗いてみましょう。
df = pd.DataFrame(data_sc, columns=iris_data.feature_names)
df.head()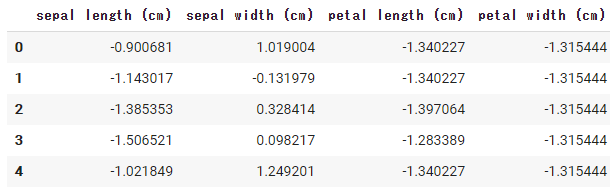
主成分分析の場合
それでは、主成分分析を使用して2次元に圧縮してみます。以下のコードを実行すると、分散説明率により、大きい順に2つの固有値を選べば90%以上の特徴を掴むことができると予想することができます。
import numpy as np
import matplotlib.pyplot as plt
cov_ = np.cov(data_sc.T) # 分散共分散行列を求めます
eigen_values, eigen_vectors = np.linalg.eig(cov_) # 固有値・固有ベクトルを求めます
plt.bar(range(1, 5), eigen_values/eigen_values.sum()) # 固有値の大きさを比較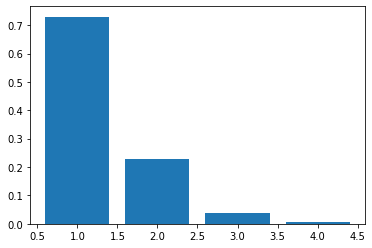
W_PCA = eigen_vectors[:, :2]
output = data@W_PCAplt.scatter(output[iris_data.target == 0][:, 0],
output[iris_data.target == 0][:, 1],
color='red')
plt.scatter(output[iris_data.target == 1][:, 0],
output[iris_data.target == 1][:, 1],
color='green')
plt.scatter(output[iris_data.target == 2][:, 0],
output[iris_data.target == 2][:, 1],
color='blue')
plt.show()
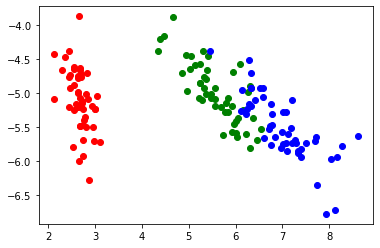
プロットの結果、4次元上の分布を2次元に圧縮しても3つに分割可能な内部表現を主成分分析では獲得できることが分かります。
不完備線形オートエンコーダの場合
それでは、次のような不完備線形オートエンコーダを定義してアヤメのデータを学習させてみたいと思います。
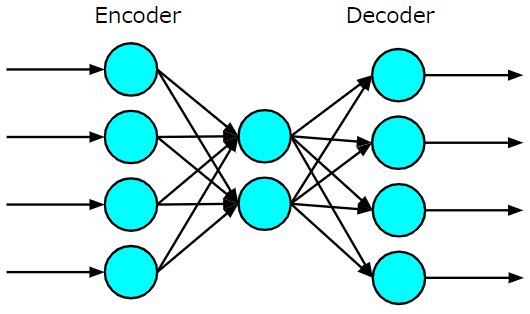
まずは、モデルを定義します。
import torch
from torch import nn
from torch import optim
# 図のような不完備線形オートエンコーダのモデルを定義
model = nn.Sequential()
model.add_module('encode', nn.Linear(4, 2, bias=False)) # 4次元から2次元に写像
model.add_module('decode', nn.Linear(2, 4, bias=False)) # 2次元から4次元に写像
print(model)
loss = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=0.01)Sequential( (encode): Linear(in_features=4, out_features=2, bias=False) (decode): Linear(in_features=2, out_features=4, bias=False) )
データをTorchで学習可能な形に変換し、反復的に学習をさせていきます。
from torch.utils.data import DataLoader
# PyTorchのモデルを学習させるデータセットの作成
data_sc_tr = torch.Tensor(data_sc)
data_loader = DataLoader(data_sc_tr, batch_size=32, shuffle=True)
ls_history = []
epochs = 200
# 学習モードに設定
model.train()
# epochs回反復して学習
for epoch in range(epochs):
for data_ in data_loader:
optimizer.zero_grad()
outputs = model(data_)
ls = loss(outputs, data_)
# 誤差逆伝播により学習
ls.backward()
optimizer.step()
# 各エポックの最終的な二乗誤差関数の値を記録
ls_history.append(ls.data)
plt.plot(ls_history)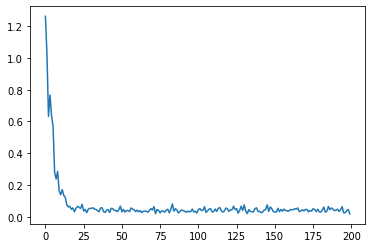
学習が終わりました。誤差関数の変化グラフを見ると、限りなく0に近い収束を見せていることが分かります。それでは、重みを抽出して、結果を可視化してみたいと思います。
# 学習結果の重みを抽出
# 次のセクションの説明で使用するので、同時にデコーダの重みも抽出します。
W_en = model.state_dict()['encode.weight']
W_de = model.state_dict()['decode.weight']output_ae = data@np.array(W_en).T
plt.scatter(output_ae[iris_data.target == 0][:, 0],
output_ae[iris_data.target == 0][:, 1],
color='red')
plt.scatter(output_ae[iris_data.target == 1][:, 0],
output_ae[iris_data.target == 1][:, 1],
color='green')
plt.scatter(output_ae[iris_data.target == 2][:, 0],
output_ae[iris_data.target == 2][:, 1],
color='blue')
plt.show()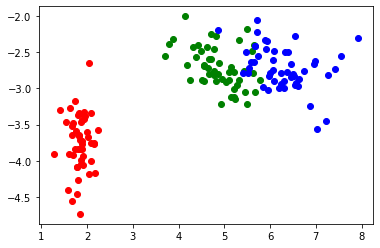
同じような位置関係に写像されていることが分かります。これは、主成分分析を使用して求めた変換行列の重みと不完備線形オートエンコーダで学習したものの重みが似ていることを意味します。実は、かなり説明を端折っていて、今回のように必ずしも似たような位置関係の写像されるとは限らない点は注意が必要です。不完備線形オートエンコーダで学習する重みは、PCAで求まる重みを回転行列により写像したものになります。そのため、重みパラメータの初期値によっては、主成分分析で得られたものとほぼ同じな場合もありますし、\(\theta\)だけ回転させたものになることもあります。再度実行すると別の位置に写像されますが、主成分分析で得られた結果を回転行列で回転させたものに対応することが見て分かると思います。式を使った詳しい説明を省略します。
エンコーダとデコーダの重みの関係
エンコーダとデコーダの重み行列は別々に用意し学習させましたが、実はデコーダの重み行列はエンコーダの重み行列を転置したものに近くなることが大抵です。先ほどの結果を見比べてみましょう。
内積をとって、正規化すれば-1から1で類似度を判断できます。
W_de = np.array(W_de)
W_en = np.array(W_en).T
(W_de*W_en).sum() / (np.sqrt((W_en*W_en).sum())*np.sqrt((W_de*W_de).sum()))0.8722717
約0.87なのでかなり類似性が高いことが分かります。オートエンコーダによっては\(\tilde{\boldsymbol{W}}^T=\boldsymbol{W}\)として重みの共有をすることがしばしばあります。自由度を制限して、雑音を学習しにくくするのに有用です。
まとめ
今回は、オートエンコーダ入門Ⅰとして、オートエンコーダの基礎的な計算式や構造上の分類を紹介し、過完備線形オートエンコーダと恒等関数、不完備線形オートエンコーダと主成分分析、重み共有について紹介しました。非線形なオートエンコーダについては、線形オートエンコーダほど単純ではないので、説明は省略しました。
オートエンコーダ入門Ⅱ回目は過完備なオートエンコーダとスパース性制約の話をしていきます。
