この記事では、ロボットの適応的な歩行を実現するときに必要となる中枢パターン生成器(Central Pattern Generator: CPG)について解説します。
こんな方におすすめ
- 動物の歩行メカニズムに興味がある
- 動物のように未知の環境でも適応的な歩行が可能なロボットを実現したい
などの方々にとって有益な内容だと思います。
適応的な行動の実現方法とは
人間社会で使用できるロボットを実現するには、ロボットが未知な環境に遭遇しても人の助けを借りずに行動を柔軟に変化させ、環境に適応できる力が必要です。つまり、歩行が可能なロボットであれば、平坦な道だけでなく、砂利道や、滑りやすい道、草むらなど、あらゆる環境においても歩行ができることが望まれます。
これは実現できない目標ではありません。なぜなら、動物は大抵の未知な環境に対しても動作を柔軟に適応させることができるからです。
ロボットの歩行を実現させるアプローチとして、以下のように2つに大別して考えてみます。
- 環境と動作を事前にモデル化する(記憶ベースの)アプローチ
- 環境に応じて自動的に行動を適応させる(学習ベースの)アプローチ
❶は、人手により事前に環境と動作について解析とモデル化を行い、それをロボットに適用する方法です。これは、解析した範囲では最適な歩行を実現できる一方で、事前に解析した環境と動作の範囲内でしか適用できないのが主な欠点になります。❷は、制御器に学習機能を持たせる手法です。未知の環境に遭遇しても数多くの試行錯誤を実行することで対応可能な行動を獲得することが期待できます。一方で、学習が望ましい動作に収束する保証がなく、また、動作の獲得に多くの試行錯誤が必要になるため、瞬時に適応的な行動を実現することは難しいというのが主な欠点になります。近年は、❶と❷を融合させた方法が一般的だと思いますが、それは今回の記事内容とは少し離れるため触れないでおきます。
簡単にまとめると、❶は未知の環境に対応できない方法で、❷は未知の環境に対応するのに時間がかかる方法になります。
動物の場合、過去の膨大な経験と感によって上手く対処している部分があるとは思いますが、未知な環境においても瞬時に適応的な行動を実現することができることは確かです。
これをロボットで実現するには、❸つ目として、未知の環境に瞬時に対応できる方法を実現する必要があります。
実は、動物はこのような機能を実現するシステムを内部に持っています。これが、本記事のテーマである中枢パターン生成器(Central Pattern Generator: CPG)です。
CPG
CPGは動物の脊髄などの中枢に存在し、歩行などのリズミックな動作において適応的な動作の生成に関与していると考えられています。
CPGはニューロン数を増やすことで複雑なリズムに対応することもできます。
神経振動子
CPGをロボットで利用するには、CPGを数理的にモデル化する必要があります。これが神経振動子モデル(Neural Oscillator: NO)です。神経振動子は、神経素子を相互抑制的に接続する相互抑制回路で実現されます。相互抑制回路は、そのパラメータを適切に調節することで、ある固有振動数で発振します。発振しているとき、ニューロンの内部状態を位相平面で可視化するとリミットサイクルを見ることができます。神経振動子は単にリズムを生成するだけでなく、フィードバックとして入力される周期信号に同調し、柔軟に固有振動数を変化させることができるという大きな特徴があります。この特徴を引き込みと呼び、適応的な動作が実現できる所以になります。
神経振動子の特徴
- リミットサイクル
- 引き込み特性
神経振動子モデルとして、以下に箇条書きで記したものがよく知られており、本記事では松岡の神経振動子モデルに主眼を置いて解説します。
- 松岡の神経振動子モデル
- 多賀の神経振動子モデル
- Williamsonの神経振動子モデル
リミットサイクル
力学系の位相空間上で閉軌道を描く運動のことをリミットサイクルと呼びます。以下にリミットサイクルの図を示します。

中心付近で閉軌道を成している部分がリミットサイクルです。今回紹介する松岡の神経振動子モデルで使用するニューロンは2つの状態変数を持ちますが、それぞれを縦軸と横軸にとって状態の変化を可視化するとリミットサイクルになっていることが確認できます(後で動画を示します)。上図のリミットサイクルの周囲に描かれている細い線は、神経振動子の初期状態がリミットサイクル上に位置しなくても滑らかにリミットサイクルへ収束する様子を表しています。
リミットサイクルは、とても安定しており、小さな摂動が加わっても、大きく崩れることはなく、元のリミットサイクルを保とうとする働きが見られます。神経振動子がリミットサイクルを示す特徴を持つということは、神経振動子に少々のノイズが加わっても、元の動作を保とうとする力学により、滑らかで適応的な挙動を生成することができることを意味します。
引き込み特性
神経振動子の固有振動数と外部から神経振動子に入力される振動数が近いとき、神経振動子の固有振動数が外部からの振動数に同調する性質を引き込みと呼びます。
松岡の神経振動子モデル
松岡さんが提案した神経振動子モデルを実装し、挙動を実際に確認してみましょう。
松岡のニューロンモデル
ここでは、松岡の神経振動子モデルで使用されるニューロン(以降、松岡のニューロンモデルと呼ぶ)について説明します。松岡のニューロンモデルは以下の図に表される構造をとります。図では1つのニューロンを示しているのですが、2つの状態変数\(u, v\)を持つモデルであるため、分かりやすく図示すると、あたかも2つのニューロンから構成されているような見た目になります。
状態変数\(u,v\)をそれぞれノードで表し、情報の流れを辺で表しています。ノードと辺の接続部分に記されいている、黒丸●と中抜きの黒丸○は、それぞれ、負の結合、正の結合を表しています。
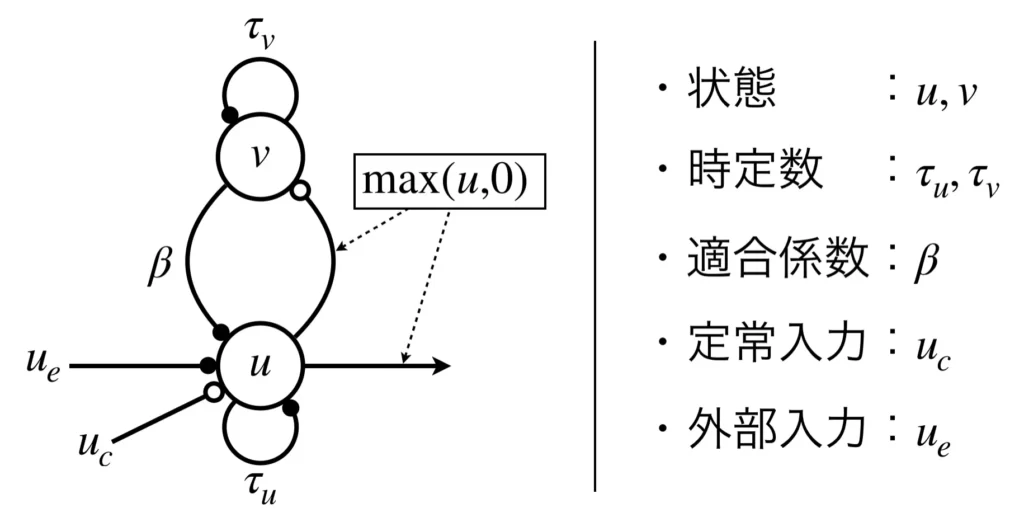
上手に示す松岡のニューロンモデルは以下の3つの式で表現されます。1つ目の式は\(u\)について、2つ目の式は\(v\)について、3つ目の式は出力についての式です。
$$\begin{eqnarray}
\tau_u\dot{u} + u &=& -\beta v + u_c - u_e\\
\tau_v\dot{v} + v &=& y\\
y &=& [u]^+
\end{eqnarray}$$
3つ目の式について補足すると、\([u]^+\)は\(\max(u, 0)\)を表しています。
松岡のニューロンモデルの図と数式を照らし合わせて確認してみてください。
松岡の神経振動子モデル
ここでは、松岡のニューロンモデルを2つ使用し、それらを抑制性結合で繋ぎ、神経振動子モデルを構築していきます。上側のニューロンは伸筋(extensor)ニューロンと、下側のニューロンは屈筋(flexor)ニューロンと呼ばれ、出力は伸筋ニューロンから屈筋ニューロンの出力を差し引いたものになります。
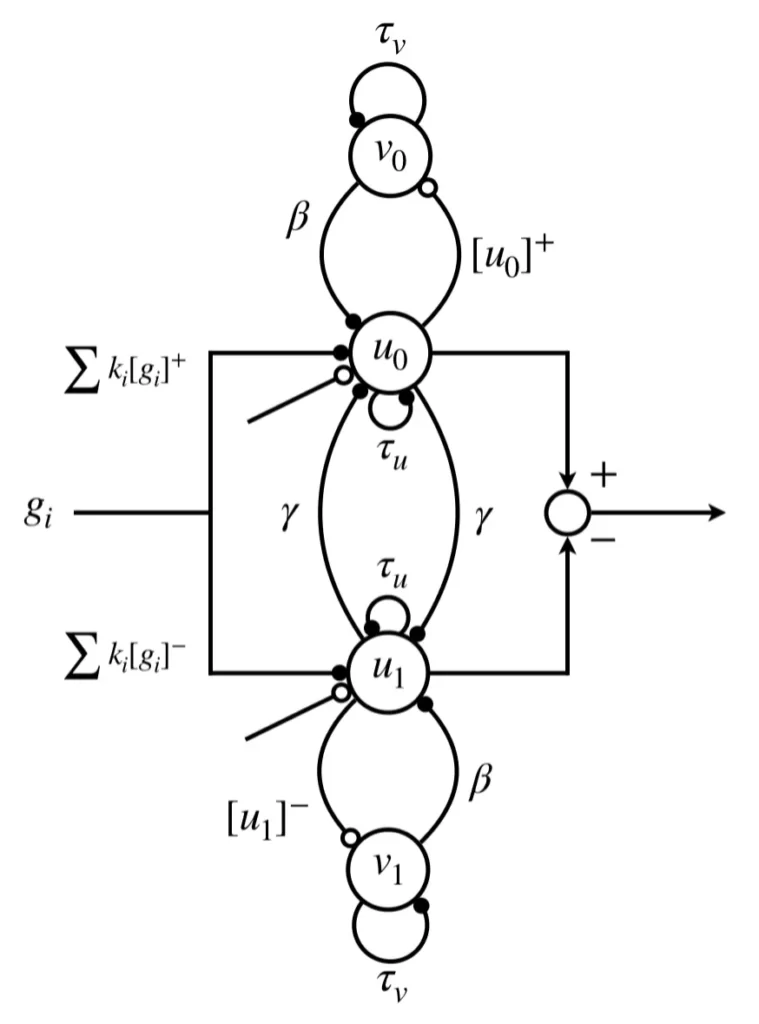
計算式は、松岡のニューロンモデルの式が2つ、ただし、外部入力\(u_e\)がそれぞれフィードバックゲイン\(\sum k_i[g_i]^+, \sum k_i[g_i]^-\)と相互結合による入力\(\gamma[u_1]^+,\gamma[u_0]^+\)の和で書き換えられたものと、伸筋ニューロンから屈筋ニューロンの出力を差し引く出力に関する式から構成されます。
$$\left\{\begin{eqnarray}
\tau_u\dot{u_0} + u_0 &=& u_c - \beta v_0 - \gamma[u_1]^+ - \sum k_i[g_i]^+\\
\tau_v\dot{v_0} + v_0 &=& y_0\\
y_0 &=& [u_0]^+
\end{eqnarray}\right.$$
$$\left\{\begin{eqnarray}
\tau_u\dot{u_1} + u_1 &=& u_c - \beta v_1 - \gamma[u_0]^+ - \sum k_i[g_i]^-\\
\tau_v\dot{v_1} + v_1 &=& y_1\\
y_1 &=& [u_1]^+
\end{eqnarray}\right.$$
$$
y_{out} = y_0 - y_1
$$
これらの式も上に示した松岡の神経振動子モデルの図と照らせ合わせることで理解できると思います。
実装コード
Pythonを使用して松岡の神経振動子モデルを実装したときの関数は以下になります。時刻\(t\)における2つのニューロンのそれぞれの状態変数(u0, v0, u1, v1)と神経振動子への入力(gain)を入力として与えることで、時刻\(t+1\)における状態変数と神経振動子の出力を得ることができます。
def matsuoka_neural_oscillator(u0, v0, u1, v1, gain, u_c=1,
beta=2.5, gamma=2.5, k=0.03,
tau_u=0.05, tau_v=0.75, dt=0.01):
# extensor neuron
dv0 = (-v0 + np.max([u0, 0])) / tau_v * dt
du0 = (u_c - u0 - beta * v0 - gamma * np.max([u1, 0]) - k * np.max([gain, 0])) / tau_u * dt
v0 = v0 + dv0
u0 = u0 + du0
# flexor neuron
dv1 = (-v1 + np.max([u1, 0])) / tau_v * dt
du1 = (u_c - u1 - beta * v1 - gamma * np.max([u0, 0]) - k * np.min([0, gain])) / tau_u * dt
v1 = v1 + dv1
u1 = u1 + du1
output = np.max([u0, 0]) - np.max([u1, 0])
return u0, v0, u1, v1, output出力の可視化
初期状態をu0=0, v0=0, u1=0, v1=0、入力を常にgain=0としたときの松岡の神経振動子モデルの出力波形を以下に示します。
リミットサイクルの可視化
同じく、初期状態をu0=0, v0=0, u1=0, v1=0、入力を常にgain=0としたときの松岡の神経振動子モデルのニューロンの状態変数(u, v)について可視化したときのアニメーションを以下に示します。
引き込み特性の可視化
実験中
最後に
本記事では、CPGの実現方法として、松岡の神経振動子モデルについて説明し、Pythonによる実装プログラムを示しつつ、挙動を紹介しました。
他にもいくつか紹介したいないことがありますが、時間を見て記事を更新していきたいと思います。
追記したい内容リスト
- パラメータを変化させたときのリミットサイクルの形状や出力波形の違い・変化
- (別記事で)四足歩行ロボットの歩行制御
