機械学習の基礎として主成分分析による次元削減について解説していきたいと思います。内容はYouTube動画による解説もアップしていますので、参考にしてみてください。
アヤメデータで主成分分析¶
主成分分析(principal component analysis:PCA)とは¶
- 分散の大きい方向(主成分)を分析すること。
- 次元削減が主な用途
※次元削減に使用されるだけで、PCA自体は次元削減のアルゴリズムではない
主成分は、分散共分散行列の固有値問題を解くことで固有ベクトルとして求まる。各々の主成分の重要度は固有値として求められる。
PCAによる次元削減¶
PCAによる次元削減の本質は、対象データの重要な特徴を限りなくそのままで、より次元の小さい特徴空間へ写像する表現行列をPCAを使用して決定することにある。 $$f:\boldsymbol{R}^n→\boldsymbol{R}^m \hspace{10mm} (n>>m)$$
なる線形写像$f$の表現行列$M$のうち、小さい次元に写像しても元のデータの重要な性質を失わない変換が可能なものを導出すること。
PCAにより求まった固有値・固有ベクトルのうち、固有値の大きい対応する固有ベクトルを少数選び、並べたものを表現行列$M$とする。
(簡単な例) In [0]:
%matplotlib inline import numpy as np import matplotlib.pyplot as plt
学習データは、
$$\boldsymbol{x_1}, \boldsymbol{x_2}, \boldsymbol{x_3}, \boldsymbol{x_4} =\left( \begin{array}{c} 1\\1 \end{array}\right), \left( \begin{array}{c} 2\\1 \end{array}\right), \left( \begin{array}{c} 2\\2 \end{array}\right), \left( \begin{array}{c} 3\\2 \end{array}\right) \in \boldsymbol{R}^2$$
In [256]:
# データの定義
data = np.array([[1, 2, 2, 3],
[1, 1, 2, 2]])
# データを表示
fig, ax = plt.subplots(figsize=(10, 7))
plt.scatter(data[0], data[1], color='blue')
ax.set_xticks([0, 1, 2, 3, 4, 5])
ax.set_yticks([0, 1, 2, 3, 4])
plt.xlim((0, 5))
plt.ylim((0, 4))
# x軸に目盛線を設定
ax.grid(which = "major", axis = "x", color = "green", alpha = 0.8,
linestyle = "--", linewidth = 1)
# y軸に目盛線を設定
ax.grid(which = "major", axis = "y", color = "green", alpha = 0.8,
linestyle = "--", linewidth = 1)
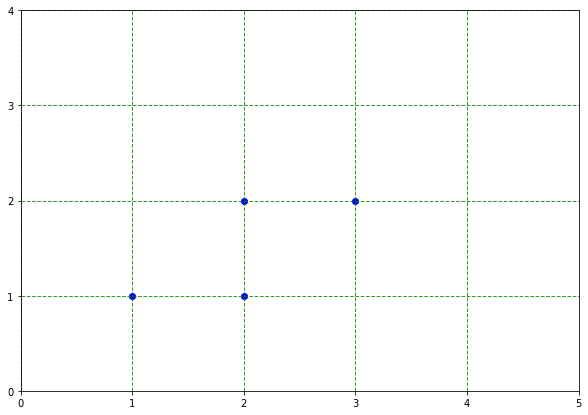
分散共分散行列を求める。平均$\boldsymbol{\overline{x}}$は、
$$\boldsymbol{\overline{x}}=\frac{1}{4}\sum_i\boldsymbol{x}_i=\left( \begin{array}{c} 2\\1.5 \end{array}\right)$$
なので、分散共分散行列は
$$
\boldsymbol{X}=(\boldsymbol{x}_1\boldsymbol{x}_2\boldsymbol{x}_3\boldsymbol{x}_4)
=\left( \begin{array}{cccc} 1&2&2&3\\1&1&2&2 \end{array}\right)
$$
$$
\boldsymbol{\overline{X}}
=\left( \begin{array}{cccc} 2&2&2&2\\1.5&1.5&1.5&1.5 \end{array}\right)
$$
として
$$\begin{eqnarray}
\Sigma &=& \frac{1}{4}(\boldsymbol{X}-\boldsymbol{\overline{X}})(\boldsymbol{X}-\boldsymbol{\overline{X}})^T\\
&=&\frac{1}{4}\left( \begin{array}{cccc} -1&0&0&1\\-0.5&-0.5&0.5&0.5 \end{array}\right)\left( \begin{array}{cc} -1&-0.5\\0&-0.5\\0&0.5\\1&0.5 \end{array}\right)\\
&=&\frac{1}{4}\left( \begin{array}{cc} 2&1\\1&1 \end{array}\right)
\end{eqnarray}$$
$$\begin{eqnarray}
\Sigma&=&\sum_i(\boldsymbol{x} - \boldsymbol{\overline{x}})(\boldsymbol{x} - \boldsymbol{\overline{x}})^T\\
&=&
\frac{1}{4}\left\{\left( \begin{array}{c} -1\\-0.5 \end{array}\right)\left( \begin{array}{c} -1\\-0.5 \end{array}\right)^T + \left( \begin{array}{c} 0\\-0.5 \end{array}\right)\left( \begin{array}{c} 0\\-0.5 \end{array}\right)^T + \left( \begin{array}{c} 0\\0.5 \end{array}\right)\left( \begin{array}{c} 0\\0.5 \end{array}\right)^T + \left( \begin{array}{c} 1\\0.5 \end{array}\right)\left( \begin{array}{c} 1\\0.5 \end{array}\right)^T\right\}\\
&=&
\frac{1}{4}\left\{\left( \begin{array}{cc} 1&0.5\\0.5&0.25 \end{array}\right) +
\left( \begin{array}{cc} 0&0\\0&0.25 \end{array}\right) +
\left( \begin{array}{cc} 0&0\\0&0.25 \end{array}\right) +
\left( \begin{array}{cc} 1&0.5\\0.5&0.25 \end{array}\right)\right\}\\
&=&\frac{1}{4}\left( \begin{array}{cc} 2&1\\1&1 \end{array}\right)
\end{eqnarray}$$
In [0]:
# デフォルトでは不偏共分散行列として求まる。nで割るか(n-1)で割るかの違いなので、問題ないが説明の都合上、biasをTrueにする。 sig = np.cov(data, bias=1)
固有値固有ベクトルを求める。 $$(\Sigma - \lambda E)\boldsymbol{v} = \boldsymbol{0}$$
$\boldsymbol{v} \ne \boldsymbol{0}$より$|\Sigma - \lambda E|=\boldsymbol{0}$なので固有方程式を解く。
$$\lambda^2-0.75\lambda+0.0625 =0$$
$$\lambda = \frac{3\pm\sqrt{5}}{8}$$
固有ベクトルは計算が面倒なので、計算機に任せるが、これにより主成分が求まる。
In [0]:
eigen_values, eigen_vectors = np.linalg.eig(sig)
In [275]:
# 固有値 eigen_values
Out[275]:
array([0.6545085, 0.0954915])
In [277]:
# 固有ベクトル(主成分) eigen_vectors
Out[277]:
array([[ 0.85065081, -0.52573111],
[ 0.52573111, 0.85065081]])
ここまでで、主成分分析自体は終了。
以降は主成分分析を使用した次元削減について説明する。
まず、固有値の大きさから重要度を測ってみる In [295]:
plt.bar(range(1, 3), eigen_values/eigen_values.sum())
Out[295]:
<BarContainer object of 2 artists>
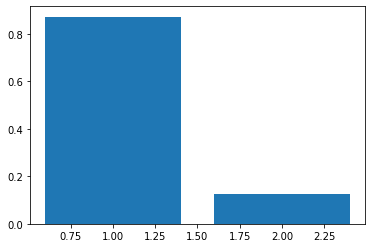
明らかに、0.6545085に対応する固有ベクトル(主成分)の方が重要度が高いことが分かる
0.0954915に対応する固有ベクトルの成分はデータから失われてもデータの本質はあまり劣化しないと仮定する。 In [0]:
data_pca = np.dot(eigen_vectors[:,0], data)
In [280]:
data_pca
Out[280]:
array([1.37638192, 2.22703273, 2.75276384, 3.60341465])
In [294]:
fig, ax = plt.subplots(figsize=(10, 7))
plt.scatter(data[0], data[1], color='blue')
plt.plot([0 + 2 - 10*eigen_vectors[:, 0][0], 10*eigen_vectors[:, 0][0] + 2],[0 + 1.5 - 10*eigen_vectors[:, 0][1], 10*eigen_vectors[:, 0][1] + 1.5])
ax.set_xticks([0, 1, 2, 3, 4, 5])
ax.set_yticks([0, 1, 2, 3, 4])
plt.xlim((0, 5))
plt.ylim((0, 4))
# x軸に目盛線を設定
ax.grid(which = "major", axis = "x", color = "green", alpha = 0.8,
linestyle = "--", linewidth = 1)
# y軸に目盛線を設定
ax.grid(which = "major", axis = "y", color = "green", alpha = 0.8,
linestyle = "--", linewidth = 1)
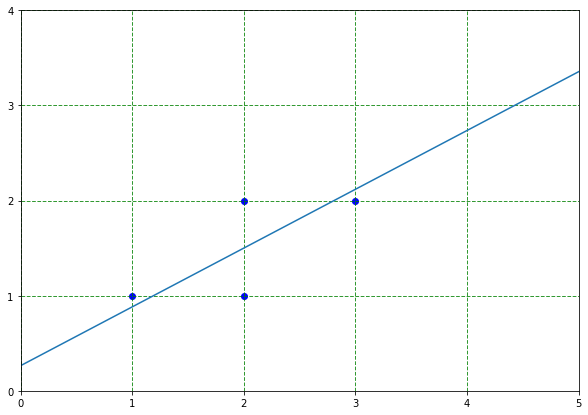
アヤメのデータでPCA¶
In [0]:
from sklearn.datasets import load_iris # アヤメのデータを読み込む iris_data = load_iris() from sklearn.model_selection import train_test_split
In [0]:
X_train, X_test, y_train, y_test = train_test_split(iris_data.data, iris_data.target, test_size=0.2, random_state=0)
In [0]:
cov_ = np.cov(X_train.T)
In [0]:
eigen_values, eigen_vectors = np.linalg.eig(cov_)
In [302]:
eigen_values
Out[302]:
array([4.34919785, 0.25228299, 0.07356191, 0.02179899])
In [303]:
eigen_vectors
Out[303]:
array([[ 0.36789541, -0.65030239, -0.59415414, 0.29789365],
[-0.07114783, -0.73234023, 0.60943602, -0.29530239],
[ 0.85398534, 0.18336024, 0.0879837 , -0.4789018 ],
[ 0.36097091, 0.08463809, 0.51752049, 0.77117374]])
In [304]:
plt.bar(range(1, 5), eigen_values/eigen_values.sum())
Out[304]:
<BarContainer object of 4 artists>
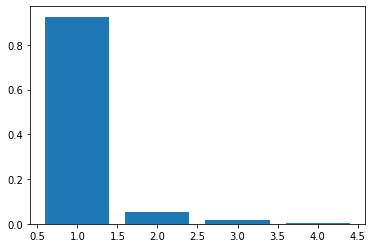
In [0]:
# ということで、最初のベクトルのみ抽出して次元削減 w = eigen_vectors[:, 0]
In [0]:
out = np.dot(w, X_train.T)
In [0]:
out_ext = np.vstack((out, np.zeros((1, len(out)))))
In [309]:
plt.figure(figsize=(15, 1))
for i in range(len(out)):
if(y_train[i] == 0):
plt.scatter(out_ext[:, i][0], out_ext[:, i][1], color='blue')
elif(y_train[i] == 1):
plt.scatter(out_ext[:, i][0], out_ext[:, i][1], color='red')
else:
plt.scatter(out_ext[:, i][0], out_ext[:, i][1], color='green')

In [0]:
from sklearn.preprocessing import StandardScaler
In [0]:
sc = StandardScaler()
In [0]:
X_train_std = sc.fit_transform(X_train)
In [0]:
cov_ = np.cov(X_train_std.T)
In [0]:
eigen_values, eigen_vectors = np.linalg.eig(cov_)
In [0]:
a = eigen_values/eigen_values.sum()
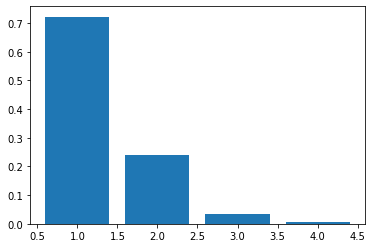
In [213]:
plt.bar(range(1, 5), a)
Out[213]:
<BarContainer object of 4 artists>
In [0]:
# ということで、最初のベクトルのみ抽出して次元削減 w = eigen_vectors[:, 0]
In [0]:
out = np.dot(w, X_train_std.T)
In [0]:
out_ext = np.vstack((out, np.zeros((1, len(out)))))
In [0]:
# ということで、最初の2つのベクトルのみ抽出して次元削減 w = eigen_vectors[:, :2]
In [0]:
out = np.dot(w.T, X_train_std.T)
In [237]:
plt.figure(figsize=(15, 10))
for i in range(len(out[0])):
if(y_train[i] == 0):
plt.scatter(out[:, i][0], out[:, i][1], color='blue')
elif(y_train[i] == 1):
plt.scatter(out[:, i][0], out[:, i][1], color='red')
else:
plt.scatter(out[:, i][0], out[:, i][1], color='green')
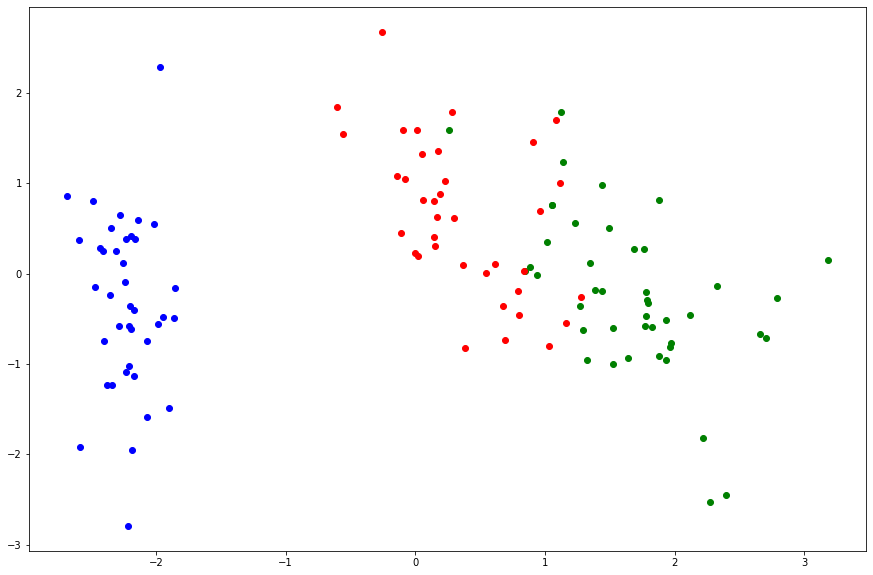
以上です
