本記事では線形写像の概要を解説したいと思います。線形写像は後に画像処理やニューラルネットワークで中心的に扱れれるアフィン写像の理解に大変重要です。以降の説明は、以下の動画でも説明していますので、必要に応じて参照してください。
※動画内のスライドに間違いがありました。以下はコピーです。
4:00頃のスライドで間違いを発見しました。 「定義域集合Vと値域集合Wの両方の空間が線形空間であるときの写像を線形写像という」 となってますが、正しくは、 「定義域集合Vと値域集合Wの両方が線形空間で、f(ax + by) = af(x) + bf(y)を満たすとき、線形写像という」 でした。
(ただいま対応動画の後悔を取りやめています)
線形空間(ベクトル空間)とは
空でない集合\(V\)が与えられたとき、和とスカラー倍が成立する空間のことを線形空間といいます。ここで、和とスカラー倍とは以下のような公理を満たしているとします。
\(\boldsymbol{x}, \boldsymbol{y}, \boldsymbol{z} \in{V}\)とするとき、「和」は以下の4つの公理を満たします。
- \(\boldsymbol{x} + \boldsymbol{y} = \boldsymbol{y} + \boldsymbol{x}\)(交換法則)
- \( (\boldsymbol{x} + \boldsymbol{y}) + \boldsymbol{z} = \boldsymbol{x} + (\boldsymbol{y} + \boldsymbol{z})\)(結合法則)
- \(\boldsymbol{x} + \boldsymbol{0} = \boldsymbol{0} + \boldsymbol{x} = \boldsymbol{x}\)なる零ベクトル(零元)\(\boldsymbol{0}\)が存在する。
- \(\boldsymbol{x} + \boldsymbol{y} = \boldsymbol{0}\)なる\(\boldsymbol{x}\)の逆ベクトル(逆元)\(\boldsymbol{y}\)が存在する。
\(\boldsymbol{x}, \boldsymbol{y} \in{V}, スカラーa, b\)とするとき、「スカラー倍」は以下の3つの公理を満たします。
- 分配法則\(\begin{align}\begin{cases} (a + b)\boldsymbol{x} &= a\boldsymbol{x} + b \boldsymbol{x}\\ a(\boldsymbol{x} + \boldsymbol{y}) &= a\boldsymbol{x} + a\boldsymbol{y}\end{cases}\end{align}\)
- \(ab\boldsymbol{x} = a(b\boldsymbol{x})\)(結合法則)
- \(1\boldsymbol{x} = \boldsymbol{x}\)
難しく見えるますが、和に成り立つ公理を4つと、スカラー倍に成り立つ公理を3つ示しただけでですので、和とスカラー倍が成り立つならば線形空間であるという理解で大丈夫です。よって、以下が成り立ちます。
線形空間である \(\Longleftrightarrow\) 和とスカラー倍が成り立つ
写像
突然ですが、\(y = f(x)\)があるとき、\(x\)の値を決めると、\(y\)の値がただ一つに定まるものを関数といいます。これを一般化したものが写像です。つまり、二つの集合が定義されているとき、定義域側の集合を構成する元の中から一つ元を決めると、値域側の集合で対応する元がただ一つに定まるものを写像といいます。
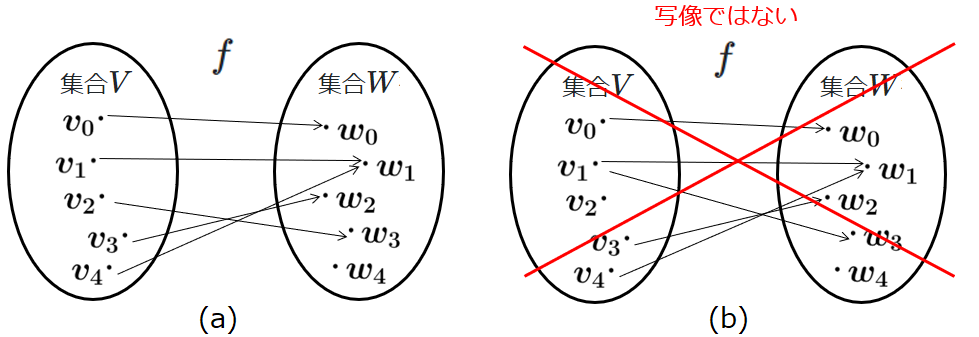
図1(a)は写像の例を、(b)は写像でない例を示しています。定義域の全ての元は値域の元に対応していなければいけません。値域のほうで重複が発生しても問題ありません。これは、\(y = x^2\)で\(x\)と\(-x\)は同じではありませんが、\(y\)が等しくなるのと同じです。一方で、(b)のように、定義域なのに、写像先の元が無かったり、ただ一つに定まらない場合は写像ではありません。
以降の説明で、集合\(V\)を定義域、集合\(W\)を値域とします。
このとき、\(f\)による写像は、
\(f:V \longrightarrow W\)
と表されます。
写像の中でも特別な場合として、単射・全射・全単射(同型写像)があります。
単射:\(\boldsymbol{x}, \boldsymbol{y} \in{V} (\boldsymbol{x} \neq \boldsymbol{y})\)のとき、\(f(\boldsymbol{x}) \neq f(\boldsymbol{y})\)
逆写像が存在するとは限らない。
全射:\(Imf = W\)
逆写像が存在するとは限らない。
全単射(同型写像):全射かつ単射でる。
逆写像が存在する。
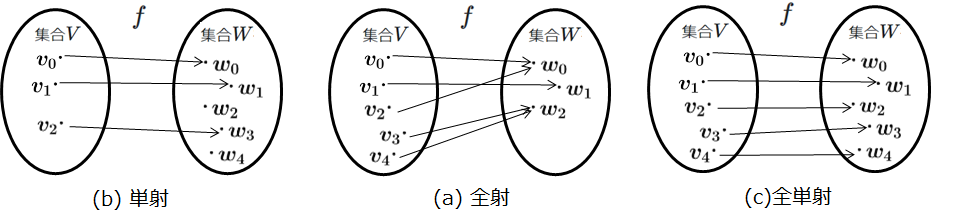
図2は単射・全射・全単射の例を示しています。次に、逆写像の存在について説明します。
関数でも、必ず逆関数が存在するとは限らない(例えば、\(x\)を実数全体したときの\(y = x^2\)など)ことと同様に、写像にも、必ず逆写像が存在するとは限りません。
分かりずらい書き方ですが、要するに、単射であり全射でないときと、全射であり単射でない場合は、逆写像は存在しません。
\(f\)の逆写像が存在 \(\Longleftrightarrow\) \(f\)は全単射
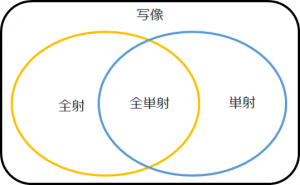
図3より、全射と単射の重なった部分が全単射であることが分かります。
線形写像
写像のなかでも、定義域集合\(V\)と値域集合\(W\)の両方の空間が線形空間のとき、 \(f(a\boldsymbol{x} + b\boldsymbol{y}) = af(\boldsymbol{x}) + bf(\boldsymbol{y})\)を満たす写像を線形写像といいます。写像の特別な場合と考えることができます。つまり、線形空間\(V, W\)の\(f\)による写像\(f:V \longrightarrow W\)は線形写像です。\(V\)を\(\boldsymbol{R}^n\)、\(W\)を\(\boldsymbol{R}^m\)とすると、\(f:\boldsymbol{R}^n \longrightarrow \boldsymbol{R}^m\)と表すこともできます。
以下の式は線形写像であるための必要十分条件です。
線形写像である\(\Longleftrightarrow f(a\boldsymbol{x} + b\boldsymbol{y}) = af(\boldsymbol{x}) + bf(\boldsymbol{y})\)
定義域の線形空間内の二つの元\(\boldsymbol{x}\)と\(\boldsymbol{y}\)の線形結合で表されたベクトル\(a\boldsymbol{x} + b\boldsymbol{y}\)を線形写像したものは、写像先の線形空間の、対応する元\(f(x)\)と\(f(y)\)の同様の係数\(a\)と\(b\)による線形結合で表されます。

図4では、線形空間の特徴である零元が定義され、零元は零元に写像されることを強調しました。
線形変換
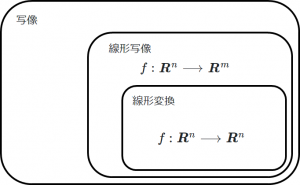
\(m = n\)つまり、\(f:\boldsymbol{R}^n \longrightarrow \boldsymbol{R}^n\)となる線形写像を線形変換といいます。つまり、線形写像の特別な場合が線形変換です。図に表すと、図5のようになります。
まとめ?
今回は、数式をあまり使用せずに概要のみを説明しました。次は、例を示しながら像、核や表現行列について説明していきたいと思います。
