機械学習の基礎としてオートエンコーダと主成分分析について解説していきたいと思います。 内容はYouTube動画による解説もアップしていますので、参考にしてみてください。
オートエンコーダと主成分分析¶
オートエンコーダ(自己符号化器)とは¶
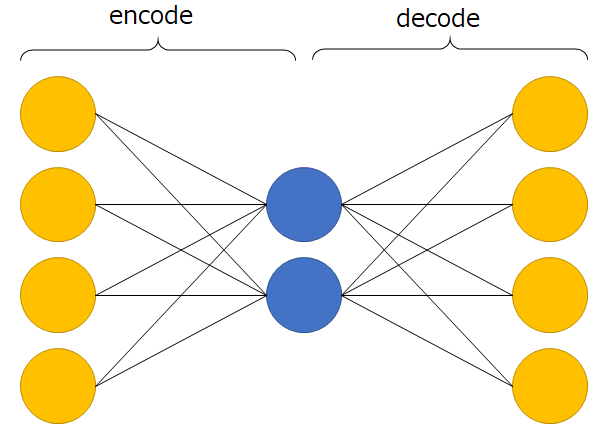
オートエンコーダ(以降AE)は一般的に上の図のようなニューラルネットワークである。中心の層の出力を符号とみなし、前半のネットワークは入力を符号化、後半のネットワークは復号化をする。AEのメインは次元削減による特徴抽出だが、もちろん符号を出力する層の数が入力層より小さくないといけないという制約はなく、より大きな次元に符号化することも可能だ(ただし使用する活性化関数には注意が必要)。AEの本質は、入力層に入力データを入れた時、出力層から入力層と同じ出力が得られるように、教師なし学習することである。
※符号化とは元のデータが復元できるように別のデータへ変換することで、主に圧縮の場で使用される。
※AEは出力層へ教師データを”別途”用意する必要がない点で教師なし学習だが、出力層に入力データを目標データとして与えているため教師あり学習であるとの見方も可能で、書籍により立場が多少異なる場合がある。
※ちなみに、ニューラルネットワークの発展は多層パーセプトロンを起源とするものと、制約ボルツマンマシンを起源とするものがあり、AEが後者を起源とする。起源は異なれど、ネットワークのグラフ構造や最適化手法が同じであるため、意識して分けて考える必要はない。
(まとめ)AEとは
- 出力層から入力データが出力できることを目標に教師なし学習するもの
- メイン用途は教師なし学習による次元削減
次元削減により特徴を自動で抽出してくれるということに帰着
SAEと事前学習¶
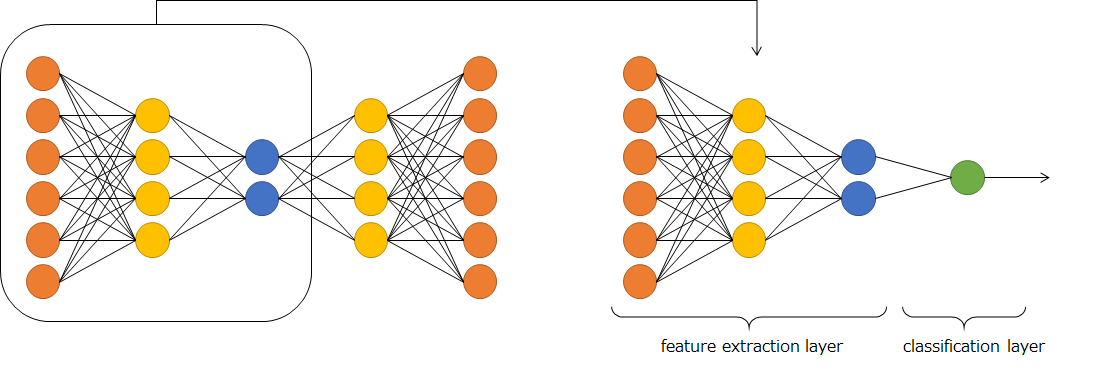
左の図は多層オートエンコーダ(stacked autoencoder;SAE)を示している。右はSAEによる事前学習を利用した深層ニューラルネットワーク(Deep Neural Network;DNN)を示している。深層になればなるほど、誤差が下位の層に伝播しない現象が起こる(勾配消失問題)。出力層に近い層しか学習ができず、下位の層は全く意味をなさない状況で、深層ニューラルネットワークの本領発揮ができていない状況だ。DNNの出力層以外は特徴抽出層であるという解釈の下、考えると、下位の層はSAEによる教師なし学習で特徴抽出ができるように変換しておけば、深層ニューラルネットワークの本領が発揮できる。これがオートエンコーダによる事前学習である。
AEの数式表現¶
今回は以下のような簡易的なオートエンコーダを扱う。
まずは、以降で使用する記号について定義しておきたい。
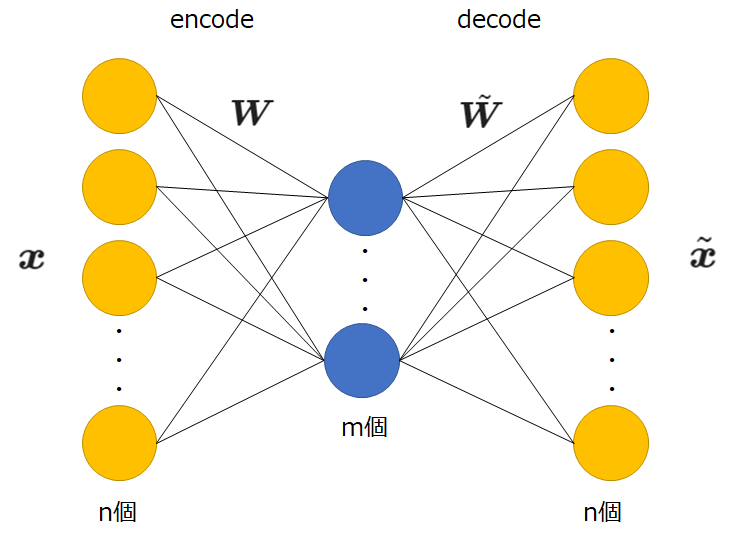
\(\boldsymbol{W}\):入力層と中間層の間の重み(m×n行列)
\(\boldsymbol{b}\):中間層ユニットの閾値(m次元ベクトル)
\(\phi\):中間層ユニットの活性化関数
\(\tilde{\boldsymbol{W}}\):中間層と出力層の間の重み(n×m行列)
\(\tilde{\boldsymbol{b}}\):出力層ユニットの間の重閾値(n次元ベクトル)
\(\tilde{\phi}\):出力層ユニットの活性化関数
\(\boldsymbol{x}\):入力データ(n次元列ベクトル)
\(\tilde{\boldsymbol{x}}\):出力データ(n次元列ベクトル)
\(\boldsymbol{X}\):入力データを行列形式で表現したもの
\(\tilde{\boldsymbol{X}}\):出力データを行列形式で表現したもの
このとき、出力は
$$\tilde{\boldsymbol{x}}=\tilde{\phi}(\tilde{\boldsymbol{W}}\phi(\boldsymbol{W}\boldsymbol{x}+\boldsymbol{b})+\tilde{\boldsymbol{b}})$$
となる。ここで、今回はPCAとの比較を行いたいため、活性化関数として恒等関数を使うと、
$$\tilde{\boldsymbol{x}}=\tilde{\boldsymbol{W}}(\boldsymbol{W}\boldsymbol{x}+\boldsymbol{b})+\tilde{\boldsymbol{b}}$$
となります。今回使用する式です。
AEの学習¶
学習には二乗誤差関数を使用します。
MNISTデータの0と1を784次元から2次元に圧縮してみよう¶
データセットを作成¶
# MNISTデータを読み込む
from keras.datasets import mnist
(X_train, y_train), (X_test, y_test) = mnist.load_data()
# 必要なライブラリをインポート
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
# bool値マスクを使用して0と1のデータを抽出
X_train_zero = (X_train[(y_train == 0)].reshape(-1, 784)).T
X_train_one = (X_train[(y_train == 1)].reshape(-1, 784)).T
新たなデータセットを作成します。ここでは教師データも作成しますが、次元削減等の学習では使用せず、次元削減結果が正しく行われたかの確認のみに使用します。
t_0 = np.zeros(1000) # 0のデータの教師信号は0
t_1 = np.ones(1000) # 1のデータの教師信号は1
#PCA用
X_train_new = np.hstack((X_train_zero[:, :1000], X_train_one[:, :1000]))
#AE検証用データ
X_val = np.hstack((X_train_zero[:, 1000:1100], X_train_one[:, 1000:1100]))
t = np.hstack([t_0, t_1])
PCAでやってみる¶
# PCAで使用するライブラリをインポート
# 分散共分散行列を求める
cov_mat = np.cov(X_train_new, bias=1)
# 固有値・固有ベクトルを求める
eigen_vals, eigen_vecs = np.linalg.eig(cov_mat)
# 入力データの次元が784なので、固有値固有ベクトルは784個存在
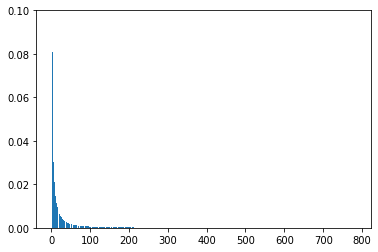
plt.bar(range(1, 785), eigen_vals/eigen_vals.sum())
plt.ylim([0, 0.1])
全ての主成分の分散説明率を示した。より十よな特徴を説明している主成分の分散説明率をみるために、範囲をかなり狭めて再度表示させる。
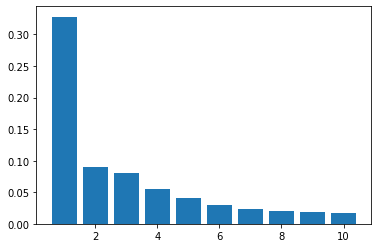
# 範囲を狭めて表示
plt.bar(range(1, 11), eigen_vals[:10]/eigen_vals.sum())
ここから、eigen_vecs[:, 0]が大変価値のある情報を捉えていうと考えられる。
PCAによって得られた主成分から2次元に写像する表現行列をPCA_Wとして保持しておく。
PCA_W = np.real(eigen_vecs[:, :2])
np.linalg.norm(PCA_W, axis=0) # ともに単位ベクトルで出力させていることが分かる
pca_x, pca_y = np.real(np.dot(PCA_W.T, X_train_new))
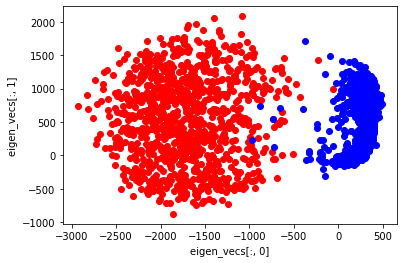
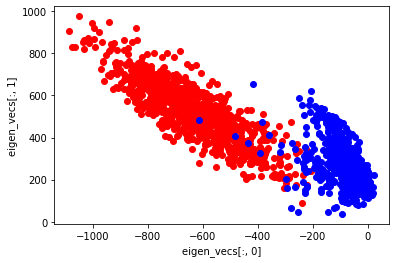
plt.scatter(pca_x[:1000], pca_y[:1000], marker="o", color='Red', linestyle='None') # 0に対応する点
plt.scatter(pca_x[1000:], pca_y[1000:], marker="o", color='Blue', linestyle='None') # 1に対応する点
plt.xlabel("eigen_vecs[:, 0]")
plt.ylabel("eigen_vecs[:, 1]")
eigen_vecs[:, 0]の特徴は$x$軸上に現れている。3割以上の分散説明率があるだけあり、はっきりと、両者の分布の違いが分かれたことが分かる。
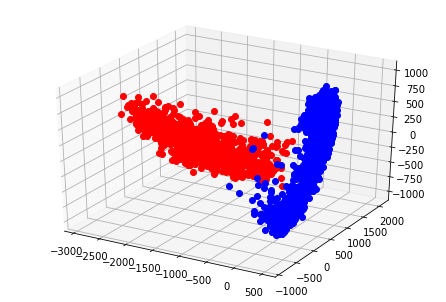
ちなみに、3次元にプロットしてみると以下のようになる。
from mpl_toolkits.mplot3d import Axes3D
x, y, z = np.real(np.dot(eigen_vecs[:, :3].T, X_train_new))
fig = plt.figure()
ax = Axes3D(fig)
ax.plot(x[:1000], y[:1000], z[:1000], marker="o", color='Red', linestyle='None') # 0に対応する点
ax.plot(x[1000:], y[1000:], z[1000:], marker="o", color='Blue', linestyle='None') # 1に対応する点
AEでやってみる¶
from tensorflow.keras.layers import Input, Dense
from tensorflow.keras.models import Model
from tensorflow import keras
enc_dim = 2
inp = Input(shape=(784, ))
encode = Dense(enc_dim, activation='linear')(inp)
decode = Dense(784, activation='linear')(encode)
AE = Model(inp, decode)
AE.summary()
AE.compile(loss=keras.losses.mean_squared_error, optimizer='sgd')
AE.fit(X_train_new.T/255, X_train_new.T/255, batch_size=128, epochs=1000, shuffle=True, validation_data=(X_val.T/255, X_val.T/255))
学習が終わったところで、AEの重み行列の値を取得する。
AE_W = AE.layers[1].get_weights()[0]
np.linalg.norm(AE_W, axis=0)
共に単位ベクトルでないことが分かる。単位ベクトルに正規化する。
AE_W /= np.linalg.norm(AE_W, axis=0)
ae_x, ae_y = np.dot(AE_W.T, X_train_new)
plt.scatter(ae_x[:1000], ae_y[:1000], marker="o", color='Red', linestyle='None') # 0に対応する点
plt.scatter(ae_x[1000:], ae_y[1000:], marker="o", color='Blue', linestyle='None') # 1に対応する点
plt.xlabel("x")
plt.ylabel("y")
直行行列と回転行列
def AE_W_(theta):
R_theta = np.array([[np.cos(theta), -np.sin(theta)],
[np.sin(theta), np.cos(theta)]])
return np.dot(R_theta, AE_W.T)
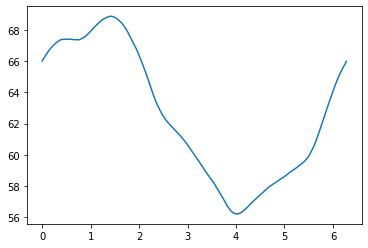
x = np.arange(0, 2*np.pi, 0.01)
error = []
for i in x:
error.append((np.abs(PCA_W.T - AE_W_rot(i))).sum())
plt.plot(x, error)
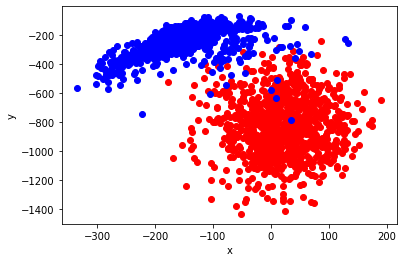
xx, yy = np.dot(AE_W_rot(4), X_train_new)
plt.scatter(xx[:1000], yy[:1000], marker="o", color='Red', linestyle='None') # 0に対応する点
plt.scatter(xx[1000:], yy[1000:], marker="o", color='Blue', linestyle='None') # 1に対応する点
plt.xlabel("eigen_vecs[:, 0]")
plt.ylabel("eigen_vecs[:, 1]")
PCAの重みをオートエンコーダに使用すると文字を復元できるのか?¶
主成分分析により得られた重みと、オートエンコーダの学習により得られた重みが近い値になることを示したかったのですが、上手く示せなかったので、最後に、主成分分析の結果得られた行列を使用してオートエンコーダを構成し、入力データを再現できるか実験していきます。
enc = np.dot(PCA_W.T, X_train_new)
dec = np.dot(PCA_W, enc)
plt.figure(figsize=(15, 10))
for i in range(4):
plt.subplot(2, 4, 2*i+1)
plt.imshow(X_train_new[:, 500*i-1].reshape((28, 28)), cmap=plt.cm.gray_r)
plt.subplot(2, 4, 2*i + 2)
plt.imshow(dec[:, 500*i-1].reshape((28, 28)), cmap=plt.cm.gray_r)
周囲の色抜きの部分が中間色の灰色になり、0の時は0が黒く、反対に1が白抜きになっている。同様に1の時は1が黒く、反対に0が白抜きになっている。